Бис­сек­три­са рав­но­сто­рон­не­го тре­уголь­ни­ка равна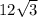
Най­ди­те сто­ро­ну этого тре­уголь­ни­ка.

Биссектриса равностороннего треугольника является медианой и высотой. Обозначим сторону треугольника буквой х.

Биссектриса равностороннего треугольника разбивает его на два равных прямоугольных треугольника, гипотенуза треугольника равна х, биссектриса является одним катетом, длина второго катета равна х/2.

По теореме Пифагора: х² = (x/2)² + (12√3)².

х² = x²/4 + 144 * 3.

х² - x²/4 = 432.

(4х²)/4 - x²/4 = 432.

(3х²)/4 = 432.

3х² = 432 * 4;

3х² = 1728;

х² = 1728/3 = 576.

х = √576 = 24.

ответ: сторона треугольника равна 24.

Объяснение:

24

Объяснение:

Пусть x - сторона равностороннего треугольника.

Биссектриса в равностороннем треугольнике является высотой и медианой, значит, в треугольнике образуется треугольник со сторонами x, (1/2)x, 12√3

По теореме Пифагора:  

x²=(1/4)x²+144*3

(3/4)x²=432

x²=576

x=24