1. Геометрия
  2. Бісектриса кута а прямокутника

Бісектриса кута а прямокутника abcd перетинає його більшу сторону bc у точці м . визначте раліус кола у см, описаного навколо трикутника, якщо вс= 24 см, ам= 10√2см

bWn bWn    1   05.09.2019 21:57    18

Ответы
dgotshalk dgotshalk  06.10.2020 20:05

Поскольку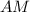 AM - биссектриса прямого угла, то 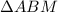зABM — равнобедренный прямоугольный треугольник, т.е.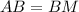 AB=BM

AB=BM=\dfrac{AM}{\sqrt{2}}=\dfrac{10\sqrt{2}}{\sqrt{2}}=10~_{\sf CM}

По теореме Пифагора из прямоугольного треугольника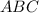 ABC

AC=\sqrt{BC^2+AB^2}=\sqrt{24^2+10^2}=26~_{\sf CM}

Центр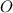 O лежит на середине диагонали 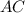AC, следовательно,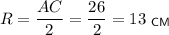 R=\dfrac{AC}{2}=\dfrac{26}{2}=13~_{\sf CM}

ответ: 13 см.


Бісектриса кута а прямокутника abcd перетинає його більшу сторону bc у точці м . визначте раліус кол
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
znatokchok znatokchok  30.10.2020 17:57
Окружность задана уравнением (х - 1)2 + у2 = 4. Постройте эту окружность. Напишите уравнение прямой, проходящей через центр окружности и точку М, с координатами М (-3;-1)...
F1Na1Ik F1Na1Ik  30.10.2020 18:07
Точки K і L належать відрізку AB, довжина якого = 40 см. Знайдіть довжину відрізка KL якщо AL = 30 см, а BK = 18 см Дайте будь ласка малюнок і повне рішення....
ariana76 ariana76  30.10.2020 18:07
В трапеции ABCD AD - большее основание. Через вершину В прове- дена прямая, параллельная стороне CD и пересекающая сторону ADв точке Е. ВС = 7 cm, AE = 4 cm. Найдите: 1) среднюю...
070974zZ 070974zZ  14.11.2019 09:22
Авсавс - прямая призма,угол acb = 90°, ac = 8, bc = 6, v= 240.найдите sбок ​...
natalya00786 natalya00786  14.11.2019 09:21
Найдите пара равных треугольников и докажи их равенства по 3 признаку​...
olya12011 olya12011  14.11.2019 09:15
Периметр равностороннего треугольника составляет 12 см, а боковая стенка - 5 см. определите табличку., заранее ! ​...
s2702e s2702e  14.11.2019 09:15
Тіктөртбұрыш тəрізді участок шаршы тəрізді плиткалармен төселген. егер учаскенің ұзындығы мен ені 7 плиткаға арттырса, онда периметрдің бойында төселген плиткалардың санынан...
Помрлтм245 Помрлтм245  15.09.2019 18:04
Всё на фото (123123123123123)-чтобы было 20 символов...
Ladylia Ladylia  15.09.2019 18:04
Запишите все делители числа 90. какие из них являются простыми? ​...
Азека2008 Азека2008  15.09.2019 18:05
Периметр квадрата равен 36см. чему равна его площадь? напишите с ,,дано буду признателен...

Популярные вопросы