Більша діагональ прямокутної трапеції є бісектрисою гострого кута. Сума основ трапеції дорівнює 31 см, а сума бічних сторін - 25 см.
Знайдіть основи та висоту трапеції.

Основания трапеции 13 см и 18 см, высота — 12 см.

Объяснение:

Так как основания трапеции — параллельные линии, а ее диагональ — секущая, то углы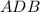 и 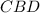равны как накрест лежащие. Таким образом в треугольнике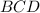 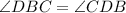, то есть и .

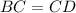Пусть . Тогда из условия , .

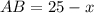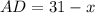Опустим высоту .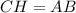

, поэтому .

Из теоремы Пифагора для треугольника CHD

Первый корень не подходит по смыслу задачи ().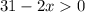

Тогда