Бічні грані правильної шестикутної піраміди нахилені до основи під кутом 30°. Радіус кола, описаного навколо основи 5 см. Знайти площу бічної поверхні. А) 50 см2 Б) 75 см2 В) 100 см2 В) 120 см2
Другие вопросы по теме Геометрия
Популярные вопросы
- Complete the sentences in your own words. HELP ME!Пример: The plane took off and...
3 - Выберите верные утверждения А. Одежда должна быть удобной Б. В зимнее время обувь...
3 - разделить текст на абзацы....
2 - Какие есть последствия подделок экономических благ...
2 - Скажите какова главная мысль сказки ПРО КОРОЛЯ И СОЛДАТА...
3 - Ребята отправились в пеший поход,который длился три дня.В первый день они пятую...
2 - Соченение на тему 《что я имею》...
2 - Эту страницу умоляю вся надежда на вас...
1 - Сочинение с любой ситуацией с использованием местоимения себя...
3 - Определите и запишите основную мысль текста. Текст 2 (1)И все-таки был художник,...
3
S бічної поверхні =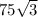 сантиметрів квадратних
сантиметрів квадратних
Объяснение:
Дано: Правильна шестикутна піраміда, R = 5 см, α = 30°(α - бічні грані правильної шестикутної піраміди нахилені до основи під кутом α)
Знайти:
S - ?(площу бічної поверхні)
Розв'язання: Розглянемо правильний шестикутник ABCDEF. Проведемо відрізки OD і OE і розглянемо трикутник Δ DOE, який буде рівнобедренним тому, що OD = OE (OD = OE = 5см за умовою), як радіуси описаного кола.Позначимо середину відрізка DE у точці M і з вершини O проведемо відрізок OM - який буде медіаною. За умовою ∠HMO = α.За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, а так як OM⊥DE, то OM є радіусом вписаного кола.У правильного шестикутника 6 сторін, а отже шість центральних кутів, нехай центральний кут β, тоді ∠DOE = β, усі 6 центральних кутів утворють повне коло отже ∠DOE = β =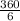 = 60°.
= 60°.
Так як OM - бісектриса за властивістю рівнобедренного трикутника, то
∠DOM = ∠MOE = ∠DOE : 2 = 60° : 2 = 30°.OM є висотою, тоді
sin ∠MOE =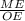 ⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
cos ∠MOE =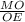 ⇒ MO = cos ∠MOE * OE = cos 30° * OE =
⇒ MO = cos ∠MOE * OE = cos 30° * OE = 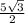 =
= 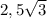
Проведемо відрізок OH - який буде висотою за властивісью шестикутної піраміди.РозглянемоΔ MOH.
cos ∠MOH = cos α =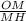 ⇒ MH =
⇒ MH = 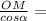
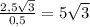 .
.
За властивістю правильної піраміди усі її грані є рівними рівнобедренними трикутниками, отже Δ HDE - рівнобедренний.Проведемо відрізок HM - який є медіаною так як DM = ME, За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, отже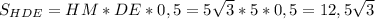 .
.
S бічної поверхні = 6 *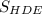 =
= 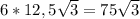 .
.