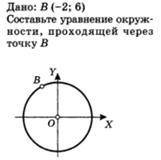
B (-2; 6) составьте уравнение окружности проходящей через точку B

Чтобы составить уравнение окружности, через данную точку B (-2; 6), нам нужно знать координаты центра окружности и ее радиус. В данном случае нам не известен радиус, но мы можем найти его с помощью другой известной точки на окружности. Сначала найдем расстояние между точками B (-2; 6) и центром окружности (x; y). Используем для этого формулу расстояния между двумя точками: d = √((x2 - x1)^2 + (y2 - y1)^2), где (x1, y1) - координаты точки B (-2; 6), (x2, y2) - координаты центра окружности (x; y). Подставим в формулу известные значения: d = √((x - (-2))^2 + (y - 6)^2). Теперь мы знаем расстояние d между точкой B и центром окружности, но он равен радиусу. Поэтому наше уравнение будет иметь вид: √((x - (-2))^2 + (y - 6)^2) = r. Теперь находим квадрат обеих частей уравнения, чтобы избавиться от корня: (x - (-2))^2 + (y - 6)^2 = r^2. Таким образом, уравнение окружности, проходящей через точку B (-2; 6), будет иметь вид: (x + 2)^2 + (y - 6)^2 = r^2. Так как мы не знаем конкретное значение радиуса r, то итоговое уравнение окружности будет выглядеть следующим образом: (x + 2)^2 + (y - 6)^2 .