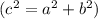Апофема правильной шестиугольной пирамиды равна 2/2, все боковые ребра пира-
миды наклонены к основанию под углом 450.
Найдите объем пирамиды.
Другие вопросы по теме Геометрия
Популярные вопросы
- Расчитайте массовую долю ортофосфата калия в 500 г его водного раствора,если...
2 - Права человека связаны с: а) гражданством б) фактом рождения в) общей...
3 - Велосипедист ехал из пункта а в пункт в со скоростью18 км/ч прибыл на...
3 - Составить уравнения реакций(овр,ионные) p--p2o5--kh2po4--k3po4 назвать...
2 - Is your town or village situated on the flat land or in the mountains...
2 - Мощность двигателя автомобиля 80 квт. при силе тяги двигателя 10 кн он...
1 - Определить массы и количества гидроксида naoh и соляной кислоты, необходимых...
1 - Буду всем ! такое: подберите имена существительные с такими признаками...
2 - Скорость моторной лодки 35.3/4 км/ч. скорость течения реки 2.1/2км.ч...
3 - Сообщение на тему спрос и предложение...
3
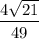 ед³.
ед³.
Объяснение:Обозначим данную правильную шестиугольную пирамиду буквами .
.
Проведём высоту пирамиды .
.
Проведём апофему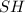 к
к 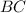 .
.
=======================================================
Так как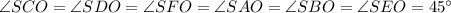 и
и 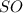 - высота ⇒
- высота ⇒ 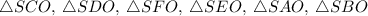 - прямоугольные и равнобедренные.
- прямоугольные и равнобедренные.
Пусть - катет этих треугольников. Тогда сторона основания пирамиды тоже
- катет этих треугольников. Тогда сторона основания пирамиды тоже  .
.
Выразим проекцию апофемы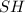 , как высоту
, как высоту 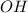 правильного
правильного  со стороной
со стороной  :
:
В прямоугольном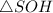 гипотенуза -
гипотенуза - 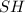 , а катет -
, а катет - 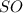 .
.
И по теореме Пифагора