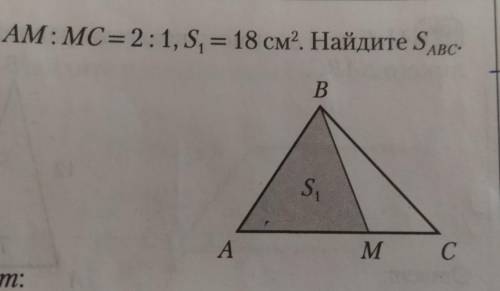
Al 35 AM: MC= 2:1, S. = 18 CM? Hainute SABC B S: A M C ответ: 410 nd C

72 см²

Объяснение:

ΔАВС подобен ΔАВМ (∠А - общий, сторона АВ - общая, АМ/МС=2/1)

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Коэффициент подобия k=2:1=2.

SABC/SABМ=2²

SABC/18=4

SABC=18*4=72 см²

можно идти к ответу разными путями. через подобие треугольников, но эта задача уже решена данным , или через площади треугольников ΔАВМ и ΔАВС по формуле половины произведений сторон на синус угла между ними или по формуле половины произведений оснований на высоту,  которая для треугольников равна, но в обоих случаях, видим,  что угол А у треугольников АВМ и АВС общий, значит,

площади относятся как SΔАВМ/SΔАВС =

((АВ*AМsin∠A)/2):((АВ*AС)sin∠A)/2)=АМ/АС, т.к. АМ:МС=2/1, то АМ/АС=2/3, тогда площадь искомая  равна 18*3/2=27/см²/

ответ 27 см²