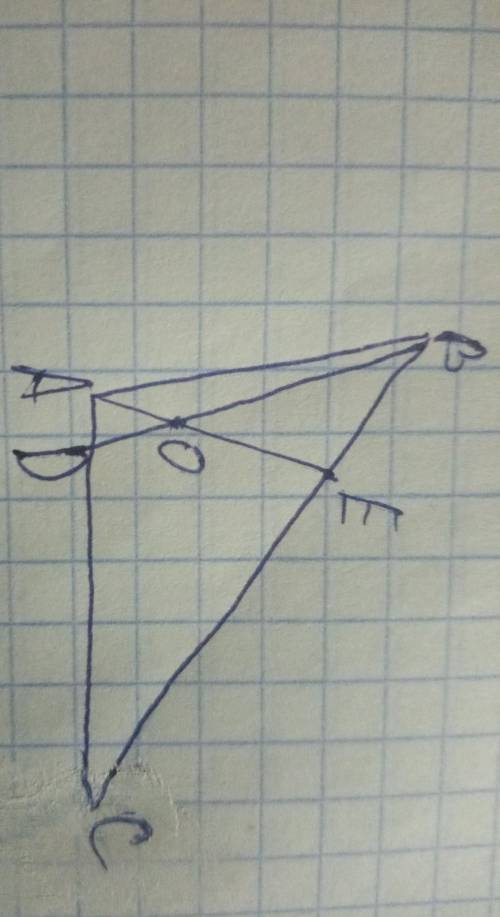
AE перпендикулярно BC, BD перпендикулярно AC. Назовите все пары подобных треугольникови докажите их подобие. Решите

~ᎪᎻᏏᏦᎪ~ Афигеть...

Добрый день! Давайте разберем этот вопрос пошагово, чтобы ответить на него подробно и обстоятельно.

Первое, что нужно учесть, это то, что перпендикулярные линии создают прямые углы. Таким образом, у нас есть два прямых угла в треугольнике ABC - угол ABC и угол BAC.

Смотря на изображение, можно заметить, что угол ABC и угол BAD являются вертикальными углами, а значит они равны. Поэтому мы можем сказать, что угол ABC равен 90 градусам.

Теперь давайте рассмотрим пары треугольников, чтобы определить, какие из них подобны. У нас есть треугольники ABE и CBD. Чтобы доказать их подобие, мы должны показать, что у них совпадают соответствующие углы и стороны пропорциональны.

1. Пара треугольников ABE и CBD:
- Углы: угол ABE и угол CBD являются прямыми углами и равны 90 градусам (так как перпендикулярные линии создают прямые углы).
- Стороны: сторона AB и сторона BC являются общими сторонами обоих треугольников.
Таким образом, у треугольников ABE и CBD совпадают соответствующие углы и одна из их сторон общая. Значит, эти треугольники подобны.

2. Пара треугольников AEB и ACD:
- Углы: угол AEB и угол ACD - это углы, образованные перпендикулярными линиями, поэтому они равны. Интересно заметить, что эти углы являются прямыми углами, так как перпендикулярные линии BC и AC создают прямые углы.
- Стороны: сторона AE и сторона AD также являются общими сторонами обоих треугольников.
Таким образом, у треугольников AEB и ACD совпадают соответствующие углы и одна из их сторон общая. Значит, эти треугольники подобны.

3. Пара треугольников BDA и CEA:
- Углы: угол BDA и угол CEA - это углы, образованные перпендикулярными линиями, поэтому они равны. Интересно заметить, что эти углы являются прямыми углами, так как перпендикулярные линии AB и AE создают прямые углы.
- Стороны: сторона BD и сторона CE также являются общими сторонами обоих треугольников.
Таким образом, у треугольников BDA и CEA совпадают соответствующие углы и одна из их сторон общая. Значит, эти треугольники подобны.

Теперь мы можем назвать все пары подобных треугольников, основываясь на доказанном ранее подобии:
1. ABE и CBD
2. AEB и ACD
3. BDA и CEA

Если у вас есть вопросы или нужно дополнительное объяснение, пожалуйста, спросите!