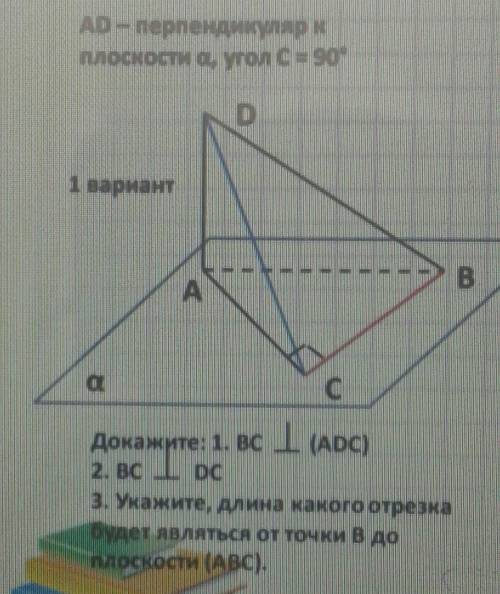
AD перпендикулярнойAD перпендикуляр к плоскости a, угол С =90° Докажите 1)BC | ( АВС)
_
2) ВС | DC
_
3) укажите длина какого отрезка будет являться от точки В до плоскости (АВС)​

Для решения данной задачи, нам понадобится использовать знания о перпендикулярах, параллельных прямых и плоскостях.

1) На данной схеме видно, что AD является перпендикуляром к плоскости ABC. Согласно свойству перпендикуляра, если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна ко всем прямым, лежащим в этой плоскости. Таким образом, можно утверждать, что BC является перпендикуляром к плоскости ABC.

2) Также на схеме видно, что BC и DC являются параллельными прямыми, так как они оба перпендикулярны к AD. Согласно свойству параллельных прямых, если две прямые параллельны третьей прямой, то они параллельны и друг другу. Таким образом, можно утверждать, что BC и DC параллельны между собой.

3) Длина отрезка BV, который является расстоянием от точки B до плоскости ABC, можно найти при помощи понятия расстояния от точки до плоскости. Для этого нам понадобится использовать формулу для расстояния от точки до плоскости:

d = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)

Где A, B и C - коэффициенты общего уравнения плоскости, а x, y, z - координаты точки B.

Так как у нас нет информации о значениях A, B, C и D, мы не можем явно вычислить длину отрезка BV. Однако, мы можем утверждать, что длина отрезка BV будет равна нулю. Это связано с тем, что BC является перпендикуляром к плоскости ABC, а прямая, перпендикулярная плоскости, лежит в этой плоскости. То есть, отрезок BV будет лежать на прямой BC, которая является перпендикуляром к плоскости ABC. Из этого следует, что отрезок BV будет иметь нулевую длину.