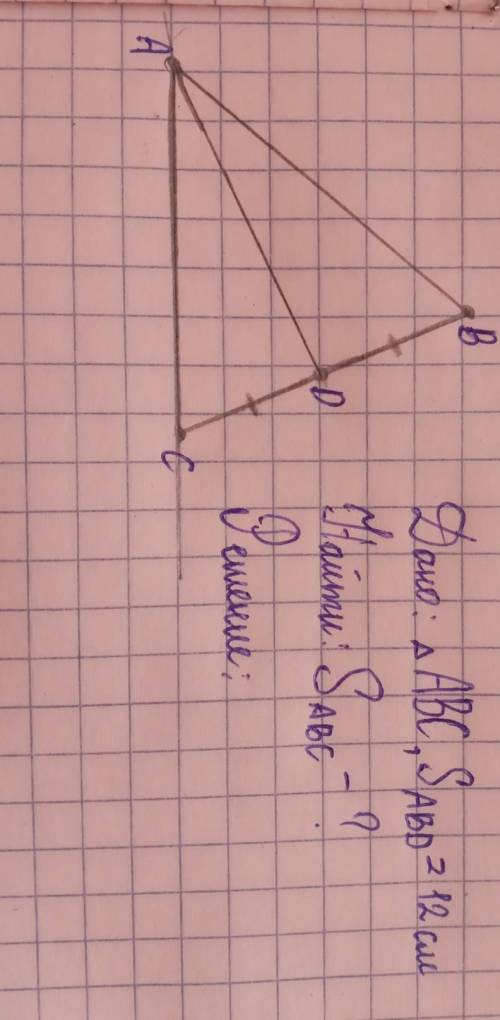
AD-медиана треугольника ABC,S аbd=12см².Найди Sabc​ решите по формуле нахождения площади

Чтобы решить эту задачу, сначала нужно понять, что такое AD-медиана треугольника. AD-медиана - это линия, которая соединяет вершину треугольника A с серединой стороны BC. То есть точка D - середина стороны BC.

Для решения данной задачи нам также нужно знать формулу для нахождения площади треугольника. Формула для нахождения площади треугольника по длинам его сторон и медиане, проведенной к одной из сторон, выглядит следующим образом:

S = (4/3) * sqrt(m * (m - a) * (m - b) * (m - c))

Где S - площадь треугольника, m - длина медианы, a, b, c - длины сторон треугольника.

Теперь применим данную формулу к нашему треугольнику ABC.

Исходя из картинки, имеем три стороны: AB, BC и AC. Известно, что AD - медиана треугольника ABC и S_abd = 12 см². Нам нужно найти S_abc - площадь треугольника ABC.

Для начала найдем длины сторон треугольника. Длина стороны AC равна сумме длин отрезков AD и DC. Так как медиана делит сторону пополам, то AD = DC. Значит, длина AC будет равна 2AD. Теперь у нас есть длины сторон AB, BC и AC.

Подставим найденные значения длин сторон и известное значение длины медианы в формулу для нахождения площади треугольника:

S_abc = (4/3) * sqrt(m * (m - a) * (m - b) * (m - c))

где m = AD, a = BC, b = AC и c = AB.

S_abc = (4/3) * sqrt(AD * (AD - BC) * (AD - AC) * (AD - AB))

Теперь осталось только подставить известные значения и решить эту формулу, чтобы получить значение площади треугольника S_abc.