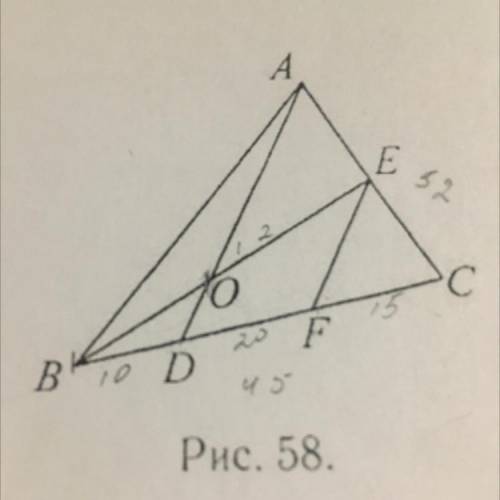
AD || EF, CB = 45, CF:FD:DB = 3:4:2, BE = 12, AC = 52 (см. рис. 58).
Найдите FD, EO, OB, CE, EA.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какую часть килограмма составляет 4 грамм? представьте свой ответ в...
2 - Дополните таблицу требующимися частями речи. переведите полученные формы...
1 - Doвывод, ответ напримеры из текста и т. п. хвост рыбы— это выводапричиныпроблемавыводфакты,...
2 - Write about a typical school day. describe what you usually do before...
2 - Решите плез соч, нужно поменять цифры, вместно 78°-63°, вместо 8 см-...
2 - Условия для создания политических режимов...
2 - Дайте определение понятию «эматизм». не менее двух примеров использования...
2 - Жұмбақ бір көзім тоқта дейді бір көзім байқа дейді бір көзім алға дейді...
1 - Объясните правописание слова разговориться...
3 - Сэтими рассчитай вторую космическую скорость, которой должен обладать...
1
Из условия задачи, мы знаем, что AD (параллельна) EF.
Сначала найдем FD:
Мы знаем, что CF:FD:DB = 3:4:2. Значит, сумма всех частей равна 3 + 4 + 2 = 9.
FD составляет 4/9 часть от этой суммы. Так как CB = 45, то FD = (4/9) * 45 = 20.
Теперь найдем EO:
EO - это отрезок между двумя параллельными линиями AD и EF. Так как DB = 20, то EO также равно 20.
Затем найдем OB:
OB - это отрезок между пересекающимися линиями AD и BE. Так как CE = 12 и CB = 45, то OB = CB - CE = 45 - 12 = 33.
После этого найдем CE:
Мы знаем, что BE = 12. Так как BE и CE образуют вертикальный угол, значит, они равны. То есть CE = 12.
И наконец, найдем EA:
EA - это отрезок между пересекающимися линиями EF и AC. Так как AC = 52 и CE = 12, то EA = AC - CE = 52 - 12 = 40.
Итак, мы получили следующие значения: FD = 20, EO = 20, OB = 33, CE = 12, EA = 40.