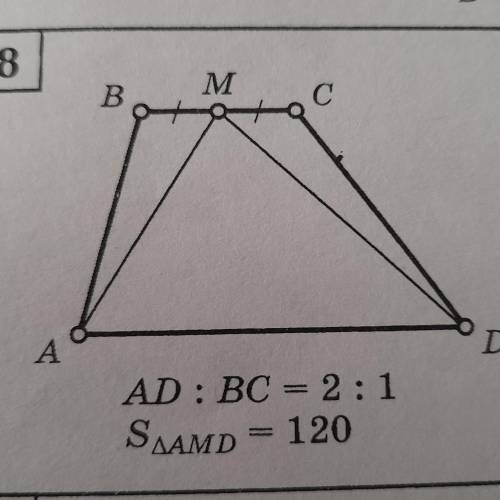
AD : BC = 2:1 S треугольника AMD = 120
найти площадь трапеции

Для решения этой задачи нам понадобится знание о соотношении сторон треугольников и площади сегментов.

Давайте разберем задачу по шагам:

1. Мы знаем, что AD : BC = 2:1. Это означает, что сторона AD в два раза больше стороны BC.

2. Мы также знаем, что S треугольника AMD (площадь треугольника AMD) равна 120. Мы не знаем высоту треугольника, поэтому обозначим ее как h.

3. Мы можем найти площадь треугольника AMD по формуле: S = (1/2) * AD * h. Подставим известные значения: 120 = (1/2) * 2 * h. Упростим выражение: 120 = h.

4. Зная высоту треугольника AMD, мы можем найти площадь трапеции. Площадь трапеции можно вычислить по формуле: S = (1/2) * (сумма оснований) * h. В нашем случае, основаниями являются стороны BC и AD.

5. Так как сторона AD в два раза больше стороны BC, то сумма оснований равна BC + AD = BC + 2BC = 3BC.

6. Подставим известные значения в формулу площади трапеции: S = (1/2) * 3BC * h. Заменим BC на h (по формуле из пункта 3): S = (1/2) * 3h * h.

7. Упростим выражение: S = (3/2) * h^2.

Таким образом, чтобы найти площадь трапеции, мы должны умножить высоту треугольника AMD на половину произведения этой высоты на 3.

Итак, ответ на задачу: площадь трапеции равна (3/2) * h^2, где h = 120. Подставим значение h в формулу: S = (3/2) * 120^2 = 3 * 60^2 = 3 * 3600 = 10800.

Таким образом, площадь трапеции равна 10800.