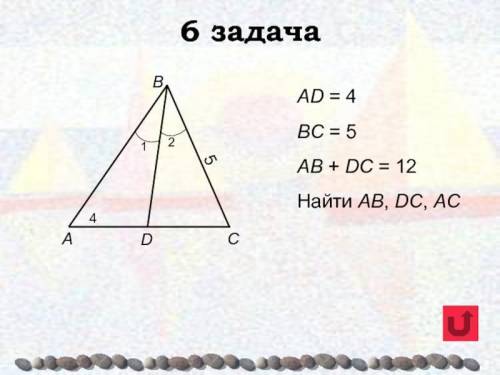
AD = 4
BC = 5
AB + DC = 12
Найти AB, DC, AC
Ответы
Добрый день! Давайте решим эту задачу вместе.
Мы имеем треугольник ABC, в котором известны следующие данные: AD = 4, BC = 5 и AB + DC = 12.
Первая информация, которая может нам пригодиться, это равенство AD = 4. Исходя из этого, мы можем предположить, что AD - это высота треугольника ABC, проведенная из вершины A.
Вторая информация - BC = 5. Мы можем предположить, что BC - это основание треугольника ABC.
Теперь давайте разберем равенство AB + DC = 12. Задача говорит нам, что сумма длин сторон AB и DC равна 12.
Мы можем использовать эту информацию, чтобы найти значение DC. Поскольку мы знаем, что AB + DC = 12, мы можем выразить DC как DC = 12 - AB.
Теперь мы можем заменить DC на (12 - AB) в равенстве AB + DC = 12 и получить AB + (12 - AB) = 12. Это упрощается до 12 = 12, что является верным утверждением.
Таким образом, мы можем сделать вывод, что значением AB и DC может быть любое число, при условии, что их сумма равна 12.
Наконец, чтобы найти значение AC, нам необходимо использовать теорему Пифагора. Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В данном случае, сторона AC является гипотенузой треугольника ABC. Мы знаем, что AD - это высота треугольника ABC, поэтому AC и AD являются катетами прямоугольного треугольника.
Таким образом, используя теорему Пифагора, мы можем написать следующее уравнение: AC^2 = AD^2 + DC^2.
Подставляя значения AD = 4 и DC = (12 - AB), мы получаем AC^2 = 4^2 + (12 - AB)^2.
Это уравнение позволяет нам расcчитать значение AC^2.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Спиши исправляя ошибки кот снежок смотрел в окно на первый снежок...
2 - При нагревании воды ее температура увеличивается. можно ли сказать, что мы:...
3 - Умальчика столько же сестер сколько братьев . а у его сестры в 2 раза больше...
3 - Арифметическая прогрессия, найти а1 дано: а2+а3=15 и 2а3-а5=9...
3 - Составить расказ на языке про лето...
1 - Чому виміряна відстань при віддаленні годинника від вуха більша ,ніж у наближенні...
2 - Подобрать и записать синонимы к данным словам с шипящих на конце слова. с...
1 - Написать сочинение 5-8 предложений на тему нужно ли нам сочувствие и сострадание...
2 - Скільки витків повинна мати вторинна обмотка трансформатора для підвищення...
1 - Построй четырехугольни abcd,если a(2- 5).b(6 7) . c(10 5).d(6 3) .что ты...
2