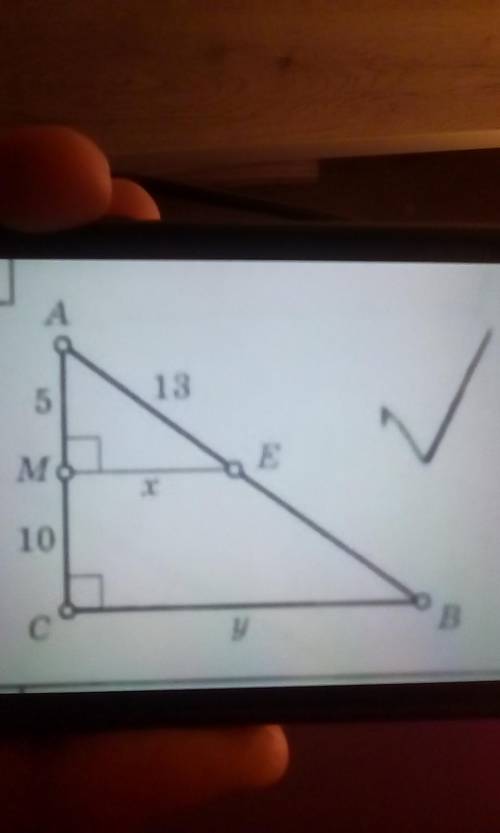
∆ ACB, AM=5, AE=13, MC=10, найти
Другие вопросы по теме Геометрия
Популярные вопросы
- Сеть с выделенным узлом – это 1. сеть с возможностью выхода в Интернет...
1 - Да, снова я. Хелп с алгеброй...
3 - ДАЮ 100Б! 1.Скриншот 2.В предложенном перечне укажите вещества, суть взаимодействия...
2 - Исправь ошибки в употреблении деепричастного оборота потеряв общественные...
3 - Виды химических реакций по отношению к количеству и составу вещества...
2 - Видношення чысел -4,5 и 0,9...
3 - Вкажіть, який орган відсутній у птахів: А) легені Б) нирки В) стравохід...
3 - КАКОВО ЗНАЧЕНИЕ ПРИЦ В ПРИРОДЕ?1.2 КАКОВО ЗНАЧЕНИЕ ПРИЦ ДЛЯ ЧЕЛОВЕКА?1.3...
3 - Постройте треугольник АВС, если сторона АС равна 7 см, сторона СВ равна...
3 - В школе 55 пятиклассников. Две пятых всех пятиклассников поехали на экскурсию...
2
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (стороны, противоположной прямого угла) равен сумме квадратов длин катетов (двух остальных сторон).
Таким образом, в нашем треугольнике можем применить теорему Пифагора:
AB^2 = AM^2 + MB^2
Поскольку нам дано AM = 5, нужно найти MB.
Для этого нам понадобится использовать отрезок AE, поскольку AM является частью него.
Заметим, что треугольник AEM прямоугольный, так как угол EAM равен прямому углу (так как E является серединой стороны BC).
Таким образом, мы можем применить теорему Пифагора для треугольника AEM:
AE^2 = AM^2 + EM^2
Поскольку нам дано AE = 13 и AM = 5, мы можем найти EM:
13^2 = 5^2 + EM^2
169 = 25 + EM^2
EM^2 = 169 - 25
EM^2 = 144
EM = √144
EM = 12
Теперь, используя найденное значение EM, мы можем найти MB:
MB = MC - EM
MB = 10 - 12
MB = -2
Теперь у нас есть длины AM и MB, и мы можем применить теорему Пифагора для нахождения AB:
AB^2 = AM^2 + MB^2
AB^2 = 5^2 + (-2)^2
AB^2 = 25 + 4
AB^2 = 29
AB = √29
Ответ: Длина стороны AB равна √29.