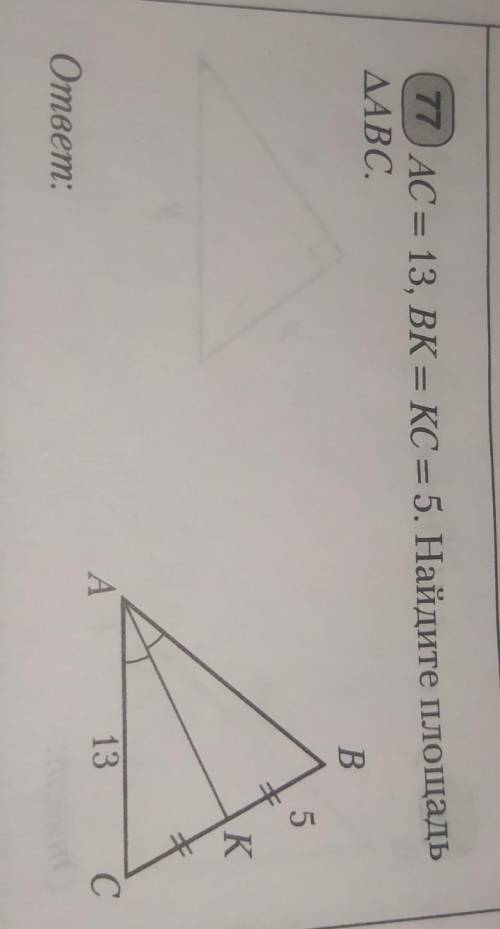
Геометрия: AC = 13, BK = KC = 5. Найдите площадь треугольника АВС.

AC = 13, BK = KC = 5. Найдите площадь треугольника АВС.

Ответы

Каракоз11111 25.01.2022 06:00

60 см²

Объяснение:

По рисунку задачи мы видим, что AK является медианой и биссектрисой, а это означает, что треугольник, равнобедренный, что даёт нам понять что и AK - высота, а зная формулу

$S=\frac{a*h}{2}$ , где h - высота

a - сторона к которой проведена высота

CB= 5*2=10 см, как CK=BK

AC=AB=13 см, ну а теперь по теореме Пифагора, мы находим сторону AK

ΔAKB(∠K=90°)

AK =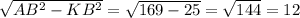 $\sqrt{AB^{2}-KB^{2}} = \sqrt{169-25} = \sqrt{144} =12$

Ну а теперь:

$S=\frac{a*h}{2} = \frac{10*12}{2} =\frac{120}{2} = 60$ см²

ПОКАЗАТЬ ОТВЕТЫ

алёночкаааа2005 25.01.2024 10:25

Для нахождения площади треугольника АВС используем формулу для вычисления площади треугольника по длинам его сторон, известную как формулу Герона.

Согласно формуле Герона, площадь треугольника можно найти по следующей формуле:

S = √(p * (p - a) * (p - b) * (p - c))

где S - площадь треугольника, p - полупериметр треугольника (полусумма длин его сторон), a, b и c - длины сторон треугольника.

Для начала, найдем полупериметр треугольника. Для этого сложим длины всех трех сторон и разделим полученную сумму на 2:

p = (AC + BK + KC) / 2

В данном случае длины сторон треугольника равны:

AC = 13
BK = KC = 5

Подставим эти значения в формулу для полупериметра:

p = (13 + 5 + 5) / 2 = 23 / 2 = 11.5

Теперь, зная полупериметр треугольника, можем рассчитать его площадь, подставив значения в формулу Герона:

S = √(11.5 * (11.5 - 13) * (11.5 - 5) * (11.5 - 5))

Выполним вычисления:

S = √(11.5 * (-1.5) * 6.5 * 6.5)
S = √(255.375)
S ≈ 15.98

Получаем, что площадь треугольника АВС примерно равна 15.98 квадратных единиц.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия