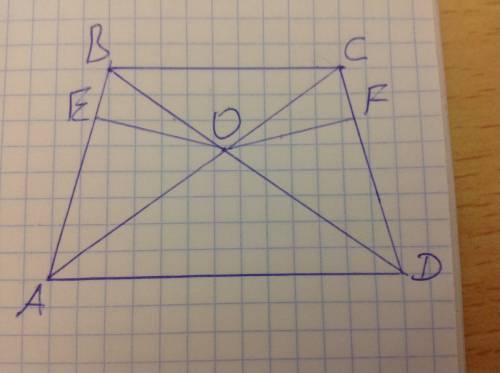
Abcd -трапеция, точка о - точка пересечения ее диагоналей, равноудалена от боковых сторон ab и cd. докажите, что трапеция равнобедренная

Докажем, что треугольники ABO и CDO равновелики (имеют равную площадь). Действительно, треугольники ABD и ACD равновелики, так как у них общее основание AD, а высоты, проведённые к этому основанию из точек B и D равны (расстояние от точки B до прямой AD равно расстоянию от точки C до прямой AD). Площадь треугольника ABO равна разности площадей ABD-AOD, а площадь треугольника CDO равна разности площадей ACD-AOD. Так как S(ABD)=S(ACD), треугольники ABO и CDO равновелики. Так как точка O равноудалена от сторон AB и CD, высоты OE и OF равны, так как OE - расстояние от O до AB, OF - расстояние от O до CD. Обозначим площадь треугольников ABO и CDO за S, тогда S=1/2*AB*OE=1/2*CD*OF. Из равенства OE=OF следует равенство AB=CD. Значит, трапеция равнобедренная, что и требовалось доказать.