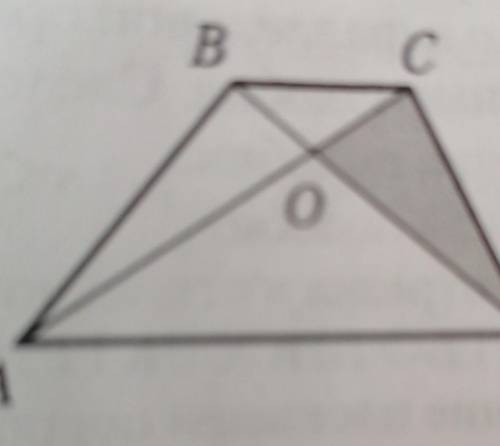
ABCD—трапеция, Sabd=18, Saod=12.
Найти Scod. ​

Чтобы найти значение Scod, нам необходимо воспользоваться свойством трапеции.

В данном случае, нам даны две диагонали трапеции и одна из боковых сторон. Мы можем воспользоваться свойством трапеции, согласно которому сумма квадратов диагоналей трапеции равна сумме квадратов ее боковых сторон.

Формула для этого свойства выглядит следующим образом:
(d1^2) + (d2^2) = (a^2) + (b^2),

где d1 и d2 - диагонали трапеции, a и b - боковые стороны трапеции.

В нашем случае, d1 = Sabd = 18, d2 = Saod = 12. Предположим, что a - это сторона AD, а b - это сторона BC.

Таким образом, мы можем записать уравнение следующим образом:
(18^2) + (12^2) = (AD^2) + (BC^2).

Вычислим значения в скобках:
324 + 144 = (AD^2) + (BC^2).

Сложим числа:
468 = (AD^2) + (BC^2).

Теперь нам нужно найти значение стороны BC, чтобы выразить Scod. У нас есть два варианта:

Вариант 1: AD = AB - BD.
Вариант 2: BC = CD - BD.

Выберем вариант 2, так как нам известны значения сторон AB, BD и CD. Заметим, что стороны AB и CD образуют прямой угол, так как трапеция ABCD является прямоугольной трапецией.

Итак, мы можем записать уравнение:
BC = CD - BD.

Подставим известные значения:
BC = 42 - 30.

Рассчитаем это значение:
BC = 12.

Теперь мы можем подставить значение BC в уравнение для трапеции:
468 = (AD^2) + (12^2).

Вычислим значение 12^2:
468 = (AD^2) + 144.

Вычтем 144 с обеих сторон уравнения:
324 = AD^2.

Теперь возьмем квадратный корень от обеих сторон, чтобы выразить AD:
AD = sqrt(324).

Рассчитаем значение sqrt(324):
AD = 18.

Теперь мы можем вычислить значение Scod, так как мы знаем, что Scod = (a + b) * h / 2, где a и b - это основания трапеции, а h - это высота трапеции.

В нашем случае, a = AD = 18, b = BC = 12. Для вычисления высоты нам понадобится использовать теорему Пифагора в треугольнике ACD.

Мы знаем, что (CD^2) = (AD^2) - (AC^2).
Подставим известные значения:
(CD^2) = (18^2) - (30^2).

Вычислим значения в скобках:
(CD^2) = 324 - 900.

Вычитаем числа:
(CD^2) = -576.

Поскольку квадрат отрицательного числа невозможен, значит, треугольник ACD вырожденный и CD = AC.

Теперь мы можем вычислить значение Scod:
Scod = (AD + BC) * h / 2.

Подставим известные значения:
Scod = (18 + 12) * CD / 2.

Приведем это уравнение к более простому виду:
Scod = 30 * CD / 2.

Рассчитаем значение 30 * CD:
Scod = 15 * CD.

Так как CD = AC, то Scod = 15 * AC.

Нам известна длина AC, она равна 30. Таким образом,
Scod = 15 * 30 = 450.

Таким образом, значение Scod равно 450.