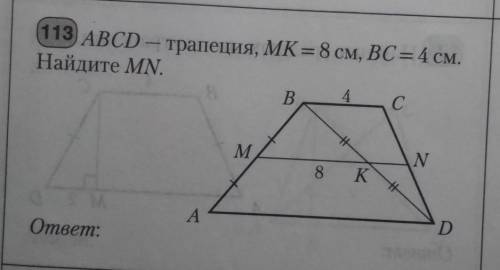
Abcd-трапеция, MK=8см, BC=4см. Найдите MN
ответ должен быть 10 см​

Для решения данной задачи, нам необходимо воспользоваться свойствами трапеции.

- Дано: Трапеция ABCD, где MK = 8 см, BC = 4 см.
- Нам нужно найти длину отрезка MN.

Шаг 1: Рассмотрим свойства трапеции ABCD.
- Сумма углов внутри трапеции равна 360 градусам.
- В трапеции ABCD параллельные стороны AB и CD.
- Признаки подобных фигур возможны.

Шаг 2: Решение.
- Из задачи нам известно, что MK = 8 см и BC = 4 см.
- Нам также дано, что AB || CD (стороны AB и CD параллельны).
- Заметим, что отрезки AM и DN являются высотами треугольников ABC и DCM, образованными между основанием трапеции ABCD и отрезком MN.
- По свойству подобных фигур, треугольники ABC и DCM подобны. Это означает, что соответственные стороны треугольников пропорциональны.

Таким образом, можно установить пропорцию между сторонами треугольников ABC и DCM, используя отношение сторон AM и DN.

AB/DC = AM/DN

- Заметим, что AM равно MK + KJ, где KJ - неизвестный отрезок.
- Аналогично, DN равно KI + IN, где KI - неизвестный отрезок.
- Подставим значения AM = 8 см и DN = MN в пропорцию:

4/x = 8/MN

- Решим пропорцию, умножив каждый член на x и MN, соответственно:

4 * MN = 8 * x

- Теперь мы знаем, что MN = (8 * x) / 4.

- Подставим данное значение MN в уравнение и решим его:

MN = (8 * x) / 4
MN = 2x

- Таким образом, мы получили, что MN = 2x.

Шаг 3: Заменяем x на 4.
MN = 2 * 4 = 8 см

Итак, мы нашли, что длина отрезка MN равна 8 см.