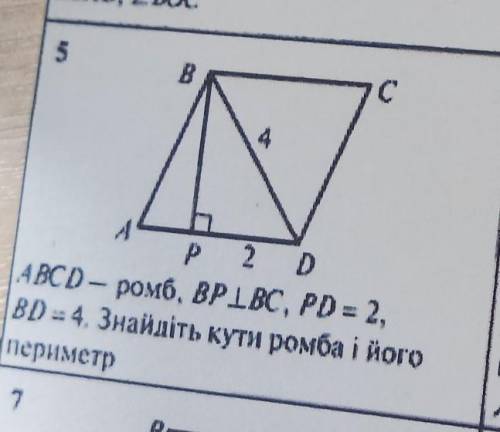
ABCD - ромб, ВР перпендикулярно ВС, PD = 2, BD = 4. Найти углы ромба и его периметр
Другие вопросы по теме Геометрия
Популярные вопросы
- Найти производную функции 1) f(x)=6x^3+2^2-182 2)f(x)=5 sin x/x...
2 - Груз массой 1 т поднимают вертикально вверх. На рисунке 2 изображен...
3 - Продолжи каждое предложение так, чтобы получились: а предложение с однородными...
3 - Что более вероятно при игре в лото: выбор 6 номеров из 49 или 5 из...
3 - Юл...ці, Анжел…ці З м яким знаком чи ні?...
3 - решить уравнение : 12 – (8 – x)2 = x (3 – x)...
1 - Ребята Решите ОДИН НОМЕР очень только сейчас решите очень кто может....
1 - КЛАСС!! Укажи предложение(я) с личным местоимением. Детский голос с...
3 - Укажите функции инфинитива в предложениях....
1 - Ціна деякого товару 450 грн.Скільки коштуватиме товар .якщо його ціну...
1
60°; 120°
Р(АВСD)=16 ед
Объяснение:
Рассмотрим треугольник ∆ВDP
BD=4 ед гипотенуза
PD=2 ед катет
Катет в два раза меньше гипотенузы, когда катет против угла 30°
<РВD=30°
Сумма острых углов в прямоугольном треугольнике равна 90°
<РDB=90°-<PBD=90°-30°=60°
Диагональ ромба является биссектриссой его углов.
ВD- биссектрисса угла <АDC
<ADC=2*<PDB=2*60°=120°
Сумма углов прилежащих к одной стороне ромба равна 180°
<ВАD=180°-<ADC=180°-120°=60°
В ромбе с углами 60°; 120°, меньшая диагональ равна стороне ромба.
ВD=AB=4ед
P(ABCD)=4*AB=4*4=16 ед.