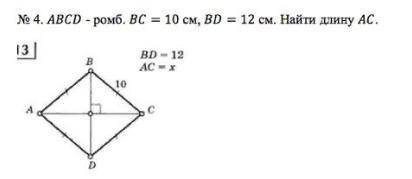
ABCD - ромб. BC = 10 см, BD = 12 см. Найти длину AC.

BD = 12
AC = x

Добрый день! Давайте решим эту задачу шаг за шагом.

Как нам известно, ABCD - это ромб, то есть все его стороны равны. Значит, AB = BC = CD = DA. В нашем случае, BC = 10 см.

Теперь нам нужно найти длину AC. Для этого нам понадобится использовать свойства диагоналей ромба.

Диагонали ромба делят его на 4 равных треугольника. Давайте рассмотрим треугольник ABC.

Мы знаем, что BD = 12 см. Так как диагональ BD - это биссектриса угла ABC, она делит треугольник на две равные части. Значит, AB = BC/2 = 10/2 = 5 см.

Теперь рассмотрим треугольник ABD. Мы знаем, что AB = 5 см, BD = 12 см. Мы хотим найти длину AC, обозначенную как x. Значит, AC = AD - DC.

Возвращаясь к свойствам ромба, мы знаем, что AD - это одна из его сторон. Значит, AD = CD = 5 см.

Теперь мы можем выразить AC, используя эти значения. AC = AD - DC = 5 - 5 = 0 см.

Ответ: длина AC равна 0 см.

Обоснование: Мы использовали свойства диагоналей ромба и равенство его сторон, чтобы рассмотреть треугольники и выразить длину AC через другие известные стороны и диагонали. В результате нашли, что AC равна 0 см. Это означает, что точка C совпадает с точкой A, и длина AC равна нулю.