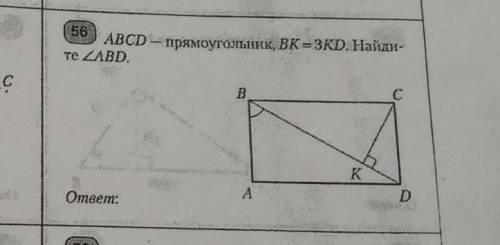
ABCD-прямоугольник,BK=3KD. Найдите угол ABD​​

вроде 90°, если ошибаюсь, то прости...

Добрый день! Рассмотрим данную задачу.

У нас есть прямоугольник ABCD, где AB и CD - стороны прямоугольника, а AC и BD - его диагонали. Также в задаче указано, что точка K находится на отрезке BD таким образом, что BK равно 3KD.

Нам нужно найти угол ABD. Для этого воспользуемся свойством диагоналей прямоугольника.

Свойство гласит: в прямоугольнике диагонали делятся пополам и пересекаются в точке, которая является их средней точкой. То есть точка K является средней точкой отрезка BD.

Теперь рассмотрим треугольник BCK. Мы знаем, что BK равно 3KD, а также, что точка K является средней точкой отрезка BD. Поэтому отношение BK к KD равно 3:1.

Вспомним синус угла в прямоугольном треугольнике: sin(угол) = противолежащая сторона / гипотенуза.

В нашем случае, противолежащей стороной является сторона BK, а гипотенузой - сторона BC (гипотенуза всегда является наибольшей стороной в прямоугольном треугольнике). Поэтому sin(угол BCK) = BK / BC.

Мы знаем, что BK равно 3KD. Подставим это значение в формулу: sin(угол BCK) = 3KD / BC.

Теперь вспомним свойства синуса. В прямоугольном треугольнике синус угла равен отношению противолежащей стороны к гипотенузе. Поэтому sin(угол BCK) = sin(угол ABD).

Таким образом, получаем: sin(угол ABD) = 3KD / BC.

Очевидно, что sin(угол ABD) равен sin(угол DAB), так как противолежащие стороны углов ABD и DAB равны сторонам KD и AD соответственно.

Получаем: sin(угол DAB) = 3KD / BC.

Теперь вспомним, что в прямоугольнике диагонали делятся пополам и пересекаются в точке, которая является их средней точкой. То есть отрезок KD равен отрезку KB.

Таким образом, у нас получается равнобедренный треугольник DKB, где KD = KB.

Это означает, что угол KDB равен углу KBD.

Рассмотрим треугольник KBD. У нас есть два равных угла KDB и KBD. Сумма всех углов в треугольнике равна 180 градусам. Поделим эту сумму поровну между равными углами: (180 градусов) / 2 = 90 градусов.

То есть угол KDB и угол KBD равны 90 градусам.

Теперь вернемся к углу DAB. У нас есть прямой угол в точке B (угол ABD равен 90 градусам), а также равные углы KDB и KBD, которые равны 90 градусам вместе. Значит, угол DAB также равен 90 градусам.

Из этого следует, что угол ABD равен 90 градусам.