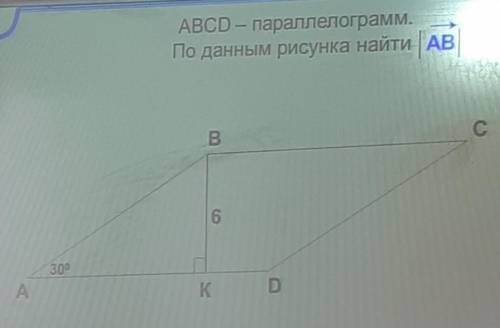
ABCD - параллелограмм. ВК- высота =6 см. Угол А=30 По данным рисунка найти вектор |АВ|. Желательно с пояснением.​

Для решения данной задачи, мы можем воспользоваться свойствами параллелограмма и использовать геометрический подход.

1. Нам дан параллелограмм ABCD, где А и В - две последовательные вершины параллелограмма, а К - точка впереди А.

2. Задача требует найти вектор |АВ|. Чтобы найти вектор, нам необходимо найти координаты начала и конца вектора.

3. Обратимся к параллелограмму ABCD. Мы знаем, что противоположные стороны параллелограмма равны и параллельны. Значит, длина стороны AB равна длине стороны CD.

4. Обратимся к высоте ВК. Мы знаем, что высота перпендикулярна к основанию (стороне AB) и образует прямой угол с ним. Также, высота разделяет параллелограмм на два равных треугольника.

5. Мы знаем, что сторона ВК равна 6 см и угол А равен 30 градусов. Для рассмотрения треугольника ВКА, мы можем использовать тригонометрию, чтобы найти сторону АК.

6. В треугольнике ВКА, у нас дан противолежащий катет VK равный 6 см. Угол А между VK и AK равен 30 градусов. Нам нужно найти гипотенузу АК.

7. Мы можем использовать тригонометрический знакомый угла 30 градусов, чтобы найти гипотенузу АК. Так как тангенс угла равен отношению противолежащего катета к прилежащему, мы можем использовать формулу:

тангенс(30) = VK / AK

тангенс(30) = 6 / AK

AK = 6 / тангенс(30)

Значение тангенса 30 градусов равно 1 / √3, поэтому:

AK = 6 / (1 / √3) = 6 * √3

8. Теперь у нас есть длина стороны AK. Чтобы найти координаты точки А, мы можем использовать координаты точки B и длины стороны AK.

9. Пусть точка B имеет координаты (x, y), тогда точка A имеет координаты (x - 6 * √3, y).

10. Значит, вектор |АВ| будет иметь координаты (x - (x - 6 * √3), y - y), то есть (6 * √3, 0)

Итак, вектор |АВ| имеет координаты (6 * √3, 0).