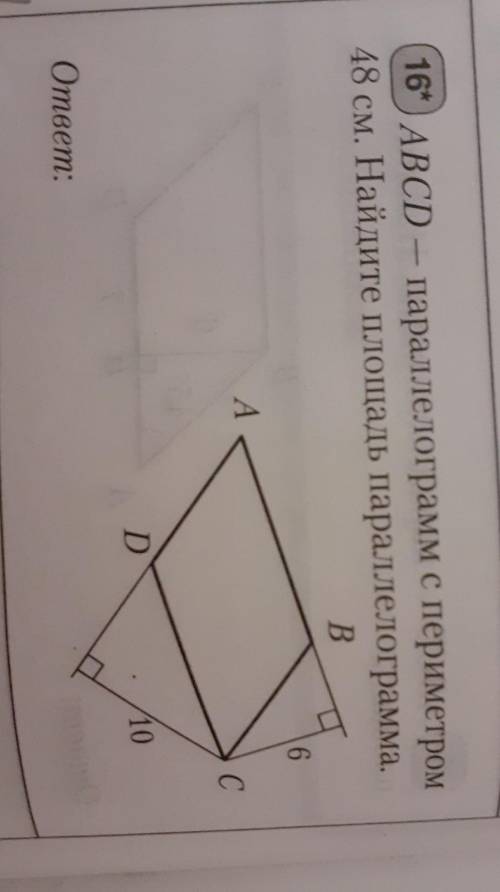
ABCD — параллелограмм с периметром
48 см. Найдите площадь параллелограмма.​

Ничего не понял!••

Добрый день!

Чтобы решить эту задачу, нам понадобится знание о свойствах параллелограмма. Одно из таких свойств гласит, что противоположные стороны параллелограмма равны по длине. Таким образом, сторона AB равна стороне CD, а сторона BC равна стороне AD.

Периметр параллелограмма равен сумме длин всех его сторон. По условию задачи периметр равен 48 см, поэтому каждая из сторон AB, BC, CD и AD равна 12 см (48 см / 4).

Теперь, чтобы найти площадь параллелограмма, нам нужно знать его высоту. Высота параллелограмма - это расстояние между параллельными сторонами, проведенное перпендикулярно к этим сторонам.

Чтобы найти высоту, можно провести линию, перпендикулярную стороне AB и проходящую через вершину D. Затем можно провести линию, перпендикулярную стороне BC и проходящую через точку A. Таким образом, мы разделим параллелограмм на два прямоугольных треугольника.

Теперь найдем площади этих треугольников. Формула для площади треугольника: площадь = (основание * высота) / 2.

В первом треугольнике основание будет равно стороне AB (12 см), а высота - это расстояние от вершины D до линии AB. То есть нам нужно найти длину линии, проведенной перпендикулярно к стороне AB и проходящей через вершину D. Здесь нам поможет знание о том, что высота параллелограмма равна расстоянию между параллельными сторонами. Таким образом, высота будет равна стороне BC (так как BC и AB - это параллельные стороны), то есть 12 см.

Теперь можем вычислить площадь первого треугольника: площадь = (12 см * 12 см) / 2 = 144 см².

Второй треугольник аналогичен первому, только его основание - сторона BC, а высота - это расстояние от точки A до линии BC. Поскольку BC и AD - это параллельные стороны, расстояние от точки A до линии BC равняется длине стороны AB, то есть 12 см. Поэтому площадь второго треугольника также будет 144 см².

Таким образом, площадь параллелограмма равна сумме площадей двух прямоугольных треугольников: 144 см² + 144 см² = 288 см².

Ответ: площадь параллелограмма равна 288 см².