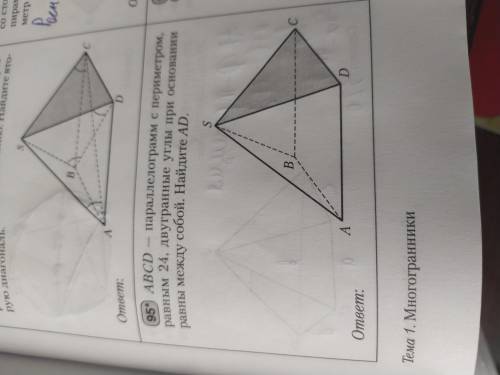
abcd - параллелограмм с периметром равным 24 см двугранный угол при основании равны между собой Найдите ad

Для того чтобы решить эту задачу, мы можем воспользоваться свойствами параллелограмма и формулами для нахождения периметра. Свойства параллелограмма: 1. Противоположные стороны параллельны и равны. 2. Противоположные углы параллельны и равны. 3. Сумма углов в параллелограмме равна 360 градусов. Дано, что периметр параллелограмма abcd равен 24 см. Периметр параллелограмма это сумма длин всех его сторон. Обозначим стороны параллелограмма следующим образом: ab = ad = x, bc = dc = y. Таким образом, получаем уравнение: 2x + 2y = 24. Для нахождения длины ad нам необходимо найти значение x. Для этого мы можем воспользоваться условием, что двугранный угол при основании равен. Обозначим угол альфа (α), который равен углу альфа1 (α1) и углу альфа2 (α2). Так как сумма углов в параллелограмме равна 360 градусов, то из условия получаем: 2α = 360 градусов, α = 360 градусов / 2, α = 180 градусов. Таким образом, находим значение угла альфа, равное 180 градусов. Используя свойство параллелограмма о равенстве противоположных углов, получаем следующее уравнение: α1 + α2 = 180 градусов, α1 = α2. Так как у нас двугранный угол при основании, то угол α1 и угол α2 равны между собой. Обозначим их оба как альфа1. Мы можем записать уравнение: α1 + α1 = 180 градусов, 2α1 = 180 градусов, α1 = 180 градусов / 2, α1 = 90 градусов. Значит, угол альфа1 (α1) равен 90 градусов. Для того чтобы нашли значение x, мы можем воспользоваться теоремой косинусов для треугольника adc. Теорема косинусов гласит: c^2 = a^2 + b^2 − 2abcos(α), где c – это сторона противолежащая углу α в треугольнике abc, а a и b – две остальные стороны треугольника. В нашем случае, треугольник adc является прямоугольным с углом α1 (α1 равен 90 градусам). Обозначим сторону ad как c, а стороны ab и dc как a и b соответственно. Тогда применим теорему косинусов для найденного треугольника: c^2 = a^2 + b^2 − 2abcos(α1). Так как у нас параллелограмм, значит a = b. Теперь подставим изначальные значения: c^2 = a^2 + a^2 − 2a^2 * cos(90 градусов), c^2 = 2a^2 − 2a^2 * 0, c^2 = 2a^2. Теперь у нас есть уравнение для c^2. Поскольку мы ищем длину ad, нам нужно найти значение c. Решим это уравнение: c^2 = 2a^2, c = sqrt(2a^2), c = a * sqrt(2). Таким образом, мы нашли длину стороны ad в терминах длины стороны ab. Следовательно, ad = a * sqrt(2). Чтобы найти значение ad, нам нужно знать значение a. Для этого вернемся к уравнению для нахождения периметра: 2x + 2y = 24. Так как ab = ad = x, а bc = dc = y, изначально получаем уравнение: 2ab + 2bc = 24. Так как ab = bc = x, мы можем записать уравнение как: 2x + 2x = 24, 4x = 24, x = 24 / 4, x = 6. Теперь у нас есть значение стороны ab, которую мы можем подставить в выражение для ad: ad = a * sqrt(2), ad = 6 * sqrt(2). Таким образом, мы находим, что ad равно 6 * sqrt(2) см. Ответ: ad = 6 * sqrt(2) см.