Abcd - параллелограмм, о - точка пересечения диагоналей, м - середина bc, da=a, dc=b выразить через векторы a и b следующие векторы a)db б) od в)ac г)dm
Другие вопросы по теме Геометрия
Популярные вопросы
- Имеет сопротивление 440 ом и рассчитан на напряжение 220 в.какое количество теплоты...
2 - Сгруппируй данные предлоги следующим образом: 1)простые непроизводные; 2)простые...
3 - Написать эссе на тему: смертная казнь за и против ( своё мнение надо обосновать)...
3 - Перечислите главные отличительные признаки растительной клетки...
3 - Разобрать слово магнитофон по составу...
2 - Дано: r1=4 ом r2=5 ом r3=10 ом r4=30 ом r5=3 ом u=40в найти: r-общию i(сила...
2 - На праздник подготовили 21 коробку конфет по 15 штук в каждой. можно ли распределить...
2 - Вповолжском районе находятся месторождения 1. железной руды 2. газа 3.нефти 4....
2 - Как правильно? вставить ноги в стремя или стремёна?...
1 - 10 олицетворений из известных произведений фольклора...
3
а)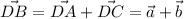
б)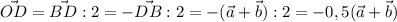
в)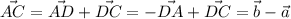
г)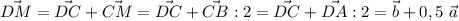
' - обозначение вектора (в моём решении).
а) DB' = DA' + DC' = a' + b' (по правилу параллелограмма).
б) OD' = OC' + CD' =AC'/2 - b' = (AD' + DC')/2 - b' = (-a' + b')/2 -b' = -(b' + a')/2
в) AC' = AD' + DC' = -a' + b'
г) DM' = DC' + CM' = b' + CB' / 2 = b' + DA' / 2 = b' + a'/2