ABC үшбұрышында АВ =1, АС=ВС=2. Үшбұрыштың АD биссектрисасы оның ВС қабырғасын бөлетін кесінділерді табыңдар
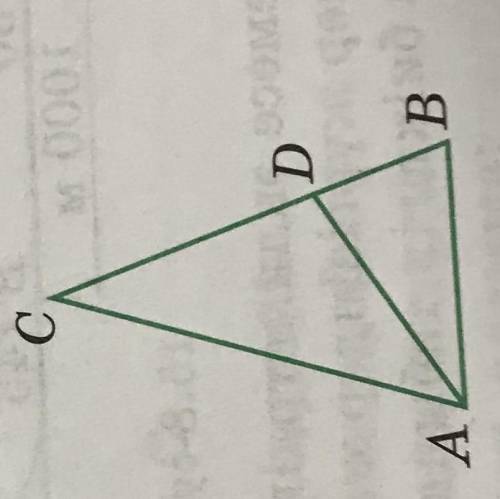
Другие вопросы по теме Геометрия
Популярные вопросы
- Почему пишется пояс с буквой я а не с е...
3 - Влетнем лагере на каждого участника полагается 40 грамм сахара в день....
2 - Назовите три группы мышц белой планарии, участвующих в изменении формы...
3 - Выпишите из любой лиирической песни невсколько строк укажите с каких средств...
2 - 3часа уже делаю связь между ос и чс, виды ос и чс...
1 - Составте текст на одну из тем. вот так морковка! летом ( осенью ) в огороде....
1 - Выражение и найдите его значение а)128+(a+472),если a=147; б)(б+168)-78,если...
3 - Напишите эссе по теме: индивидуальность-это неповторимый набор красок...
1 - Вопросы на тему члены предложений (минимум 7 предложений)...
2 - Найдите углы параллелограмма ю, если один из них в 2 раза меньше другого...
3
Давайте обозначим точку пересечения биссектрисы AD с стороной BC как точку E. Мы можем рассмотреть два треугольника: треугольник ABE и треугольник ACE. Мы знаем, что AB = 1 и AC = BC = 2.
Для начала, давайте найдем отношение длин отрезков EC и EB. По свойству биссектрисы, это отношение должно быть равно отношению длин отрезков AC и AB.
AC/AB = EC/EB
2/1 = EC/EB
2 = EC/EB
Теперь мы можем найти значения длин отрезков EC и EB, зная, что их отношение равно 2. Мы должны выбрать такие значения, чтобы их сумма была равна длине стороны BC. Давайте обозначим EB как х, тогда EC будет равно 2х.
EB + EC = BC
х + 2х = 2
3х = 2
х = 2/3
Таким образом, EB = 2/3, а EC = 4/3.
Теперь у нас есть значения длин отрезков EB и EC. Мы также знаем, что длина стороны BC равна 2. Мы можем найти длину отрезка BE, вычитая длину отрезка EC из длины стороны BC:
BE = BC - EC
BE = 2 - 4/3
BE = 2/3
Таким образом, отрезок BE равен 2/3.
Таким образом, ответ на задачу состоит в том, что отрезок BE равен 2/3.