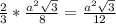ABC – равносторонний треугольник со стороной a. AM и BN – медианы треугольника, K = AM ∩ BN. Найдите площадь четырёхугольника CMKN.
Другие вопросы по теме Геометрия
Популярные вопросы
- Слова на зат есим ,сын емим 3 слова...
2 - Определи порядок действий и найди значения выражений (524*225/90-818)+62208/243...
3 - Как пишется ? ! в приём к врачу или в приём врачу ? 48 !...
3 - Найти координаты точки с, в которую переходит точка а координатами (2; 0) при повороте...
1 - Решить следующие по : 1) в прямоугольном треугольнике abc , где гипотенуза cb равна...
1 - 1.напиши свои предложения с m.v -can , may, mest , have to (три примера) 2.задай...
1 - Моржа малышка доставили в зоопарк поздней осенью. запишите название наклонения в...
1 - Сколько будет 750*250 столбиком? ? в школу через 2 часа...
2 - Принадлежат ли графику уравнения 2х-3у=2 точки а (4; 2) в (5; -2)...
2 - Докажите, что при прямолинейном равноускоренном движении без начальной скорости...
3
ABC – равносторонний треугольник со стороной a. AM и BN – медианы
треугольника, K = AM ∩ BN. Найдите площадь четырёхугольника CMKN.
Объяснение:
S( равност.)=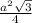 .
.
S(FBN)=S(CBN), т.к основания равны и высоты из вершины В одинаковые. S(CBN) =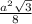 .
.
Проведем СК . S(ВМК)=S(СМК) , т.к основания ВМ=МС , а высота h -одинаковая.
S(СКN)=S(СМК) как площади равных треугольников . Равны по трем сторонам СК-общая , CN=CM ,KN=KM по свойству медиан треугольника.
Значит S(СМКN)=