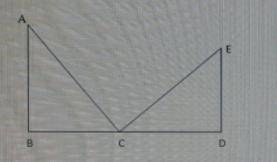
ABC и CED заданы треугольники, AB=8 BC=4 CD=4.5 найдите ED

Чтобы решить эту задачу, мы воспользуемся свойством треугольников с одинаковыми углами - подобием треугольников.

Поскольку треугольники ABC и CED имеют одинаковые углы, они подобны. Это означает, что соответствующие стороны треугольников пропорциональны.

Нам известно, что AB = 8, BC = 4 и CD = 4.5. Мы ищем сторону ED.

Чтобы найти ED, мы можем использовать пропорции. Для этого нужно найти соответствующую сторону в треугольнике CED, которая соответствует стороне AB в треугольнике ABC.

Мы можем записать пропорцию следующим образом:

AB/CD = AC/ED

Подставим известные значения:

8/4.5 = (4 + AC)/ED

Далее, чтобы найти ED, нам нужно изолировать эту переменную. Мы можем сделать это, умножив обе стороны уравнения на ED:

(8/4.5) * ED = 4 + AC

Упростим выражение:

ED = (8/4.5) * ED - 4

Теперь мы можем вычислить ED, подставив известные значения (AB = 8, BC = 4 и CD = 4.5) в уравнение:

ED = (8/4.5) * 4.5 - 4

ED = 8 - 4

ED = 4

Таким образом, длина стороны ED равна 4.