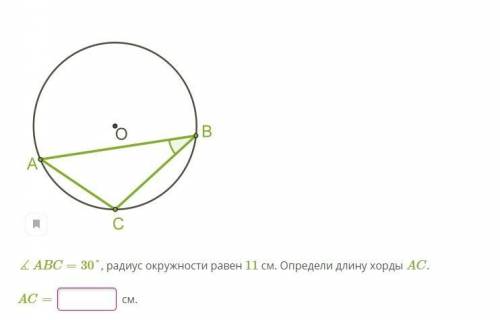
ABC=30°, радиус окружности равен 11 см. Определи длину хорды AC.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ребзи, я yt. мне ролик снимать. так вот. задали рассказать про освободителей польши....
3 - Выполнить морфологический разбор причастия (к) ра..трепа(н,нн)ой (г..лове)...
3 - Суровнением (7,85х-12,4х)*(-1 9/91)=-2 11/12-1 2/3...
1 - ответ на по 3 класс 2 часть страница 113 номер 5 б)...
2 - Составьте числовое выражение и найдите его значение. 1. 39 . произведение суммы...
3 - :а) (3х в третей, у) во второй б) (а-з) во второй - 2а(2а-3) в) (у+5)(у--5)(у+5)...
1 - Середнє арефметичне двох чисел дорівнює 69. знайтиці числа, якщо одне з них на 15...
3 - Найдите среднее арифмитическое чисел 2,8; 42,3; 7,4 и 16,5...
2 - Одна бригада может выполнить некоторую работу за 24 дня,вторая работает в 1,5 раза...
2 - Fill in the gaps with the suitable verbs in the right form. to join to do to go...
2
Сначала обратим внимание на угол ABC, который равен 30°. Нам известно, что углы, опирающиеся на одну и ту же дугу, равны. В данном случае дуга AC опирает собственно на угол ABC.
Также известно, что хорда, проведенная через центр окружности, делит ее на две равные части. В данном случае хорда AC проведена через центр окружности, так как она проходит через точку O, являющуюся центром окружности.
Используя свойство углов, мы можем сказать, что между хордой AC и радиусом OA имеется угол в 30°, так как угол ABC равен 30°.
Теперь давайте обратимся к самой хорде AC. Она делит окружность на две равные части, поэтому у нас получится два прямоугольных треугольника OAC и OBC.
Определим длину хорды AC, используя теорему косинусов для треугольника OAC. У нас имеется известная сторона AC (которую мы и хотим найти), радиус окружности OA (который равен 11 см) и угол OAC (который равен 30°).
Теорема косинусов гласит: c^2 = a^2 + b^2 - 2ab*cos(C), где c - длина стороны, противолежащей углу C, a и b - длины других двух сторон.
В нашем случае:
c - длина стороны AC (которую мы хотим найти),
a - длина стороны OA (которая равна 11 см),
b - длина стороны OC (которую мы хотим найти),
C - угол OAC (который равен 30°).
Подставим известные значения в формулу:
AC^2 = OA^2 + OC^2 - 2*OA*OC*cos(OAC).
Так как OC и OA являются радиусами окружности и равны между собой, мы можем заменить их одной величиной r:
AC^2 = r^2 + r^2 - 2*r*r*cos(30°).
Упростим:
AC^2 = 2r^2 - 2r^2*cos(30°).
Теперь заменим косинус 30° известным значением:
AC^2 = 2r^2 - 2r^2*0.866025 (так как cos(30°) = 0.866025).
Выполним вычисления:
AC^2 = 2r^2 - 1.732051r^2.
Упростим еще раз:
AC^2 = 0.267949r^2.
Подставим значение радиуса 11 см:
AC^2 = 0.267949*11^2.
Выполним вычисления:
AC^2 = 32.558732.
Чтобы найти длину хорды AC, возьмем квадратный корень от полученного значения:
AC = √32.558732.
Выполним округление до двух десятичных знаков:
AC ≈ 5.71 см.
Таким образом, длина хорды AC составляет примерно 5.71 см.