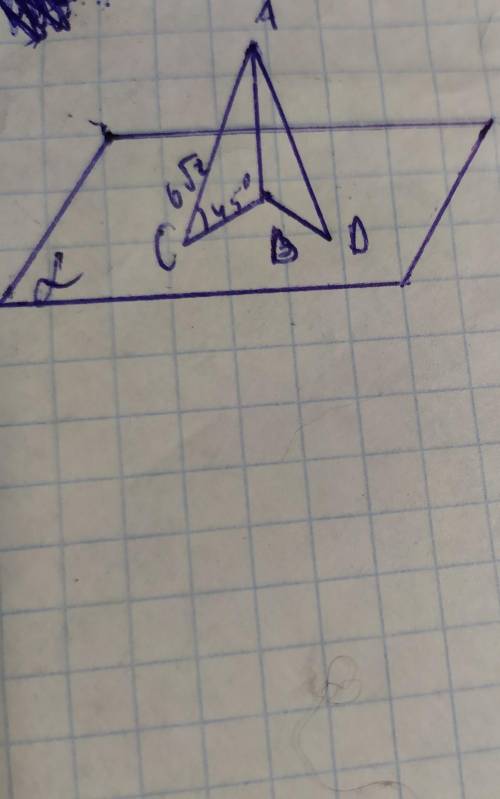
AB перпендикулярно плоскости альфа, угол ACB=45°, AC=6√2 см, BD=8 см. Тогда AD=?​

Для решения этой задачи мы можем использовать знания о геометрии треугольников и тригонометрии.

В данном случае, у нас есть треугольник ABC, в котором AB является высотой, опущенной на сторону AC. Угол ACB равен 45 градусов, и сторона AC известна равной 6√2 см. Также, мы знаем, что BD = 8 см.

Нам нужно найти длину стороны AD, то есть найти расстояние от вершины треугольника A до точки D.

Шаг 1: Воспользуемся свойством перпендикуляра. В треугольнике ABC мы знаем, что AB - это высота, опущенная на сторону AC. Это означает, что угол BAC также равен 90 градусов. Таким образом, у нас есть прямоугольный треугольник BAC.

Шаг 2: Применим тригонометрию. В прямоугольном треугольнике BAC мы можем использовать соотношение тангенса, так как у нас известна противолежащая сторона (AB) и прилежащая сторона (AC):

тангенс угла BAC = AB/AC

Тангенс угла BAC = AB/(6√2)

Так как тангенс угла BAC равен 1, мы можем записать:

1 = AB/(6√2)

Шаг 3: Решим уравнение. Чтобы найти длину стороны AB, умножим обе стороны уравнения на 6√2:

6√2 = AB

Таким образом, мы находим, что длина стороны AB равна 6√2 см.

Шаг 4: Найдем длину стороны AD. Для этого, применим теорему Пифагора в прямоугольном треугольнике ABD:

AB^2 = AD^2 + BD^2

Подставим значения, которые мы знаем:

(6√2)^2 = AD^2 + 8^2

36 * 2 = AD^2 + 64

72 = AD^2 + 64

AD^2 = 72 - 64

AD^2 = 8

AD = √8

AD = 2√2

Таким образом, мы находим, что длина стороны AD равна 2√2 см.