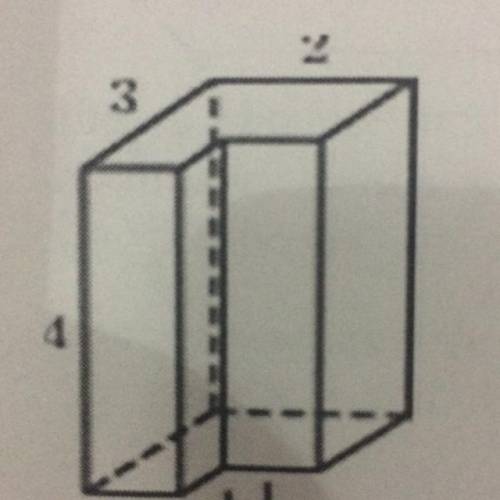
А5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

50

Объяснение:

1) Так как все двугранные углы данного многогранника прямые, то он является прямой призмой, и все его боковые грани являются прямоугольниками.

Площадь поверхности S прямой призмы равна сумме площадей её оснований S осн и боковой поверхности S бок:

S = S осн + S бок    

2) Так как все углы верхнего основания прямые, то его площадь равна разности площадей прямоугольника с размерами 3 х 2 (3 в длину, 2 в ширину) и углового выреза с размерами 1 х 1 (1 в длину, 1 в ширину):

3 · 2 - 1 · 1 = 6 - 1 = 5

А так как нижнее основание в прямой призме равно верхнему основанию, то площадь нижнего основания также равна 5, а площадь двух оснований равна:

S осн = 5 · 2 = 10

3) Площадь боковой поверхности прямой призмы S бок равна произведению периметра её основания P на высоту Н, которая в прямой призме равна длине бокового ребра (согласно рисунку, боковое ребро равно 4, следовательно, высота Н =4):

S бок = Р · H  

Р = 3 + 2 + (3-1) + 1 + 1 + (2-1) = 10

S бок = Р · H = 10 · 4 = 40  

4) Площадь поверхности многогранника, изображенного на

рисунке:

S = S осн + S бок = 10 + 40 = 50

ответ:  площадь поверхности многогранника, изображенного на

рисунке, равна 50.