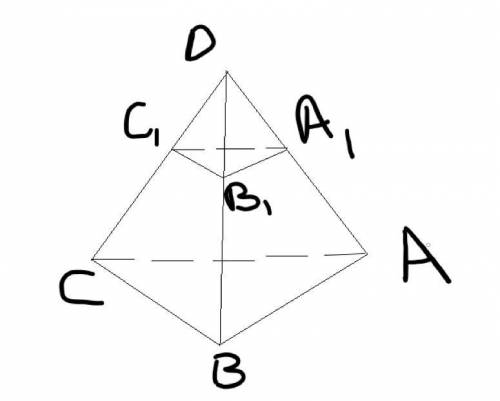
A1B1C1 || ABC, DA1 : AA1 = 3 : 4, S(A1B1C1)= 27

Найти S(ABC)

A1B1C1 || ABC, DA1 : AA1 = 3 : 4, S(A1B1C1)= 27  . Найти S(ABC)

Объяснение:

1) Т.к. плоскости граней A1B1C1 и ABC параллельны , то А1С1║АС⇒ соответственные углы ∠DC1A1=∠DCA  и ∠D-общий . Поэтому ΔDC1A1 ∼ DCA по 2 углам .В подобных треугольниках сходственные стороны пропорциональны : .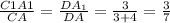

2) Т.к. A1B1C1 || ABC , то ΔA1B1C1  подобен ΔABC с коэффициентом

подобия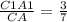       , к= 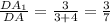.  По т. об отношении площадей подобных треугольников  

получаем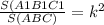  или 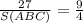   , S(ABC)=12 ед².