А) Существует ли выпуклый шестиугольник, углы которого равны 10°, 50°, 140°, 175°, 185°, 200°. ответ обоснуйте. b) Найдите внешние углы правильного семиугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Кого римляне называли «варварами»? : а) племена, не знающие латинского...
1 - Впервой канистре на 4.8л бензина больше ,чем во второй ,а в двух канистрах...
3 - Реакция гидролиза хлорида калия kcl...
3 - Решить! прочитай выражения разными сделай прикидку и найди их значения....
3 - Вы помните какие-нибудь праздники, которые традиционно празднуются в...
1 - Запиши вси двоцыфрови числа, в яких килькисть десяткив на 2 менша вид...
2 - Какое количество теплоты необходимо для нагревания железной гири массой...
2 - 1.в равнобедренном треугольнике авс с основанием ас точка m середина...
3 - Общая масса всех молекул днк в 46 хромосомах одной соматической клетки...
2 - Азотная кислота: 1)состав 2)тип и класс вещества 3)тип связи 4) свойства...
3
10 50&_&+-располагалось
а) Нет такого шестиугольника
b) Внешний угол семиугольника равен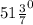 . Сумма внешних углов семиугольника равна 360°.
. Сумма внешних углов семиугольника равна 360°.
Объяснение:
а) сумма углов выпуклого многоугольника равна по формуле
S=180°(n-2)
Где n - количество углов многоугольника. Здесь n=6.
S=180°(6-2)
S=180°*4
S=720° - сумма внутренних углов шестиугольника.
Просуммируем 6 углов
10°+50°+140°+175°+185°+200°=200°+175°+185°+200°=400°+360°=760°
То есть такого выпуклого шестиугольника не существует в Евклидовой геометрии.
b) У правильного семиугольника сумма внутренних углов равна
S=180°(7-2)
S=180°*5
S=900°
Внешний угол равен
А сумма внешних углов равна