А Правильное решение каждого задания оценивается одним
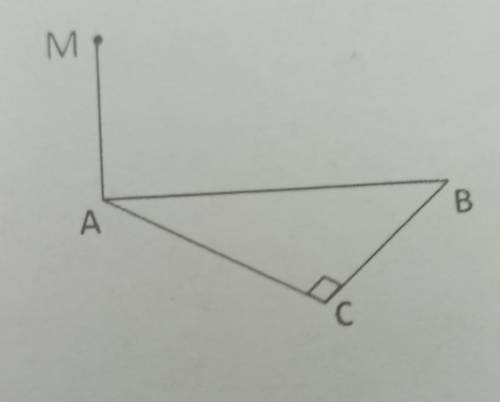
К плоскости прямоугольного треугольника ABC (ZC = 90°) проведен
перпендикуляр МА (см. рис).
Мt
1. Какой из прямых (AB, MB, MC)
перпендикулярна прямая Вс?
ответ:
2. Какой из плоскостей (АВС, МАВ, МВС)
перпендикулярна плоскость MAC?
ответ:
3. Чему равна проекция наклонной на плоскость, если наклонная,
длина которой равна 2 см, составляет с плоскостью угол 45°?
ответ:
4. Найдите диагональ куба, ребро которого равно 2 см.
ответ:
5. В кубе ABCDA,B,C,D, найдите угол между плоскостями ABC и CDD.
ответ:​

1. Чтобы определить, какая из прямых (AB, MB, MC) перпендикулярна прямой Вс, мы можем использовать свойство перпендикулярных прямых, которое гласит, что если две прямые перпендикулярны к третьей прямой, то они перпендикулярны друг другу.

Из условия мы знаем, что прямая Вс перпендикулярна к плоскости треугольника ABC, поэтому мы можем сделать вывод, что каждая линия, пересекающая эту плоскость, будет перпендикулярна прямой Вс.

Таким образом, все прямые (AB, MB, MC) являются перпендикулярными прямой Вс.

2. Чтобы определить, какая из плоскостей (АВС, МАВ, МВС) перпендикулярна плоскости MAC, мы используем свойство перпендикулярных плоскостей, которое говорит, что если две плоскости перпендикулярны к третьей плоскости, то они перпендикулярны друг другу.

Из условия мы знаем, что плоскость MAC перпендикулярна плоскости треугольника ABC. Кроме того, здесь у нас есть перпендикулярная плоскость МАВ, которая проходит через прямую Вс (как мы узнали в предыдущем пункте).

Таким образом, плоскости АВС и МВС перпендикулярны плоскости MAC.

3. Чтобы найти проекцию наклонной на плоскость, мы используем формулу проекции: Проекция = длина наклонной * cos(угол между наклонной и плоскостью).

В данном случае наклонная имеет длину 2 см и составляет угол 45° с плоскостью. Подставим эти значения в формулу:

Проекция = 2 см * cos(45°).

Теперь нам нужно вычислить значение cos(45°). Применим таблицу значений cosинуса и найдем cos(45°), который равен √2 / 2.

Теперь мы можем вычислить проекцию:

Проекция = 2 см * (√2 / 2) = √2 см.

Таким образом, проекция наклонной на плоскость равна √2 см.

4. Чтобы найти диагональ куба, мы можем использовать теорему Пифагора, которая гласит, что в прямоугольном треугольнике с катетами a и b гипотенуза c определяется по формуле c = √(a^2 + b^2).

В данном случае длина ребра куба равна 2 см. Диагональ куба является гипотенузой прямоугольного треугольника с катетами, равными длине ребра. Таким образом, мы можем записать:

c = √(2^2 + 2^2) = √8 = 2√2 см.

Таким образом, диагональ куба равна 2√2 см.

5. Чтобы найти угол между плоскостями ABC и CDD, мы можем использовать свойство угла между плоскостями. Данное свойство гласит, что угол между двумя плоскостями равен углу между их нормалями.

Нормаль к плоскости ABС можно найти, взяв векторное произведение двух векторов, лежащих в плоскости ABС, например, векторов AB и AC. Нормаль к плоскости CDD также можно найти, взяв векторное произведение двух векторов, лежащих в плоскости CDD, например, векторов CD и DD.

Угол между нормалями можно найти, используя формулу:

cos(угол) = (нормаль1 * нормаль2) / (длина нормали1 * длина нормали2),

где '*' означает скалярное произведение векторов, а длина нормали определяется как квадратный корень из суммы квадратов ее компонент.

Подставим соответствующие значения в формулу и вычислим угол.

Однако, для решения этого вопроса необходимо предоставить все заданные в условии данные, так как они могут быть неявными (например, длины векторов AB, AC, CD, DD), чтобы я мог правильно рассчитать угол между плоскостями ABC и CDD.