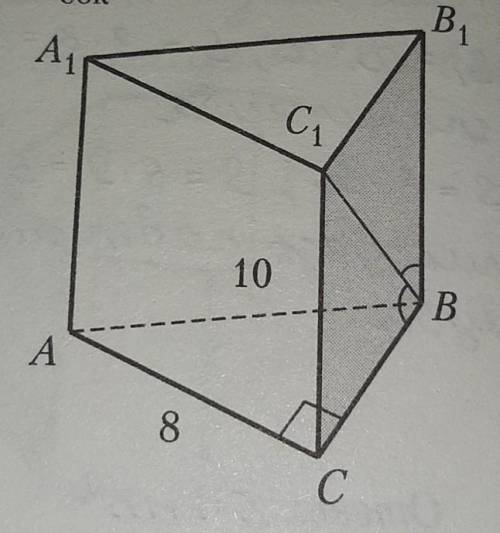
A...C1-прямая призма, BC1-биссектриса угла CBB1, угол ACB=90 градусов. Найдите площадь боковой поверхности призмы Sбок.​

Для решения этой задачи нам понадобится знание о биссектрисе угла, а также о формуле для вычисления площади боковой поверхности призмы.

В данной задаче у нас есть а..с1-прямая призма, где Bc1-биссектриса угла CBb1, а угол ACB равен 90 градусов. Нам нужно найти площадь боковой поверхности призмы Sбок.

Для начала, обратимся к определению биссектрисы угла. Биссектриса угла - это линия, которая делит данный угол на две равные части. В нашем случае, BC1 является биссектрисой угла CBB1, что означает, что два угла, образованных этой биссектрисой, являются равными.

Теперь, обратим внимание на прямоугольный треугольник ABC. Угол ACB равен 90 градусов, а значит угол BAC равен 90 градусов тоже. Это означает, что треугольник ABC - прямоугольный.

Поскольку Bc1 - биссектриса угла CBB1, то мы можем сделать вывод, что треугольник ABC и треугольник Bc1C схожи (имеют равные углы). Из этого следует, что отношения сторон этих треугольников должны быть равны. То есть, мы можем записать:

AC / BC = BC1 / Bc1C

Нам известно, что угол BAC равен 90 градусов, поэтому мы можем использовать теорему Пифагора, чтобы выразить длину AC через длины AB и BC. Теорема Пифагора гласит:

AC^2 = AB^2 + BC^2

Теперь, когда у нас есть выражение для AC, мы можем записать это в соотношение между сторонами треугольников:

(AB^2 + BC^2) / BC = BC1 / Bc1C

Теперь, решим это уравнение относительно BC1:

BC1 = (AB^2 + BC^2) * Bc1C / BC

Теперь нам нужно вычислить площадь боковой поверхности призмы. Площадь боковой поверхности призмы вычисляется по формуле:

Sбок = Периметр основания * высота

Периметр основания призмы можно найти как сумму всех сторон основания. В данном случае, это AB + BC + AC.

Высоту призмы можно найти с помощью биссектрисы угла Bc1C, так как биссектриса проходит через вершину C, а основание призмы параллельно плоскости ABc1C.

Таким образом, мы можем найти площадь боковой поверхности призмы Sбок следующим образом:

Sбок = (AB + BC + AC) * Bc1C

Вычислив все длины и подставив их в эту формулу, мы сможем найти искомую площадь боковой поверхности призмы.