A||b угол 5 больше угла 6 на 12° найдите углы 1-8​

Добрый день! Для решения данной задачи нам необходимо использовать свойства параллельных линий и их пересекающихся прямых. Давайте разберемся в подробностях.

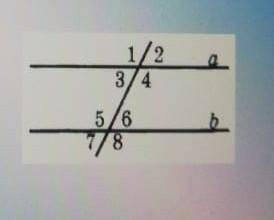
На данной картинке мы видим пару параллельных прямых, обозначенных как A и B. Мы также видим пересекающую их прямую, обозначенную цифрой 5. В задаче говорится, что угол 5 больше угла 6 на 12 градусов.

Сначала давайте найдем значение угла 6. Мы знаем, что угол 5 больше угла 6 на 12 градусов. Это означает, что если мы от угла 5 отнимем 12 градусов, то получим значение угла 6.

Угол 5 = угол 6 + 12°

Теперь давайте обратимся к параллельным линиям A и B. Когда параллельные линии пересекаются с третьей линией, называемой трансверсальной, тогда углы, образующиеся в точке пересечения, будут равными.

Угол 5 = угол 1
Угол 6 = угол 2

Теперь мы можем записать следующее:

Угол 1 = угол 2 + 12°

Но у нас есть еще одно свойство параллельных линий — смежные углы. Смежные углы — это два угла, которые имеют общую сторону и одну общую вершину, но лежат по разные стороны этой стороны. В данной задаче у нас имеются две пары смежных углов:

1. Угол 8 смежный с углом 1.
2. Угол 7 смежный с углом 2.

Мы также знаем, что смежные углы равны.

Угол 1 = угол 8
Угол 2 = угол 7

Теперь у нас есть все данные, чтобы найти значения углов от 1 до 8.

Угол 2 + 12° = угол 1
Угол 7 + 12° = угол 8

Теперь мы можем проанализировать картинку и увидим, что углы последовательно увеличиваются от 1 до 8. Поэтому, если угол 1 равен углу 2 плюс 12 градусов, то угол 2 будет равен углу 1 минус 12 градусов, и так далее.

Ответ:

Угол 1 = угол 2 + 12°
Угол 2 = угол 1 - 12°
Угол 3 = угол 2 - 12°
Угол 4 = угол 3 - 12°
Угол 5 = угол 4 - 12°
Угол 6 = угол 5 - 12°
Угол 7 = угол 6 + 12°
Угол 8 = угол 7 + 12°

Надеюсь, это решение понятно и помогает вам понять, как найти значения углов от 1 до 8 в данной задаче. Если у вас остались вопросы, пожалуйста, обращайтесь!