9.Знайдіть довжину кола описаного навколо трапеції , сторони якої дорівнюють 6 см , 6 см 6 см і 12

Ответы

stas7365w98 25.04.2021 13:13

Формула вычисления длины окружности, зная радиус окружности: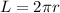 $L = 2\pi r$

Для начала определим вид треугольника.

Нам уже дано, что около трапеции однозначно описана окружность.

А окружность можно описать только около равнобедренной трапеции!.

Что и означает, что боковые стороны равны — 6; 6.

Другого выбора у нас нет, кроме как объявить, что одно из оснований ровно боковой стороне — 6, а второе основание равно: 12.

Формула вычисления радиусa описанной окружности около равнобёдренной трапеции — такова:

$R = \frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}\\p = \frac{a+d+c}{2}$

Тоесть, для вычисления этого радиуса — нам должны быть известны основания трапеции, боковая сторона, и! диагональ.

Обозначения сторон: боковые равные стороны равны: "c"; большее основание равно: "b"; меньшее основание равно: "b".

Формула вычисления диагонали равнобедренной трапеции такова: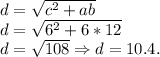 $d = \sqrt{c^2+ab}\\d = \sqrt{6^2+6*12}\\d = \sqrt{108} \Rightarrow d = 10.4.$

А в этой формуле, переменные таковы: обе боковые стороны обозначаются как "a"; верхнее основание, которое равно боковой стороне — обозначается как "b"; основание с длиной в 12 см — обозначается как "c".

Теперь, зная все стороны трапеции, и диагональ — найдём радиус: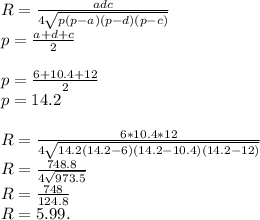 $R = \frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}\\p = \frac{a+d+c}{2}\\\\p = \frac{6+10.4+12}{2}\\p = 14.2\\\\R = \frac{6*10.4*12}{4\sqrt{14.2(14.2-6)(14.2-10.4)(14.2-12)}}\\R = \frac{748.8}{4\sqrt{973.5}}\\R = \frac{748}{124.8}\\R = 5.99.$