. 9 класс, вписанные и описанные фигуры
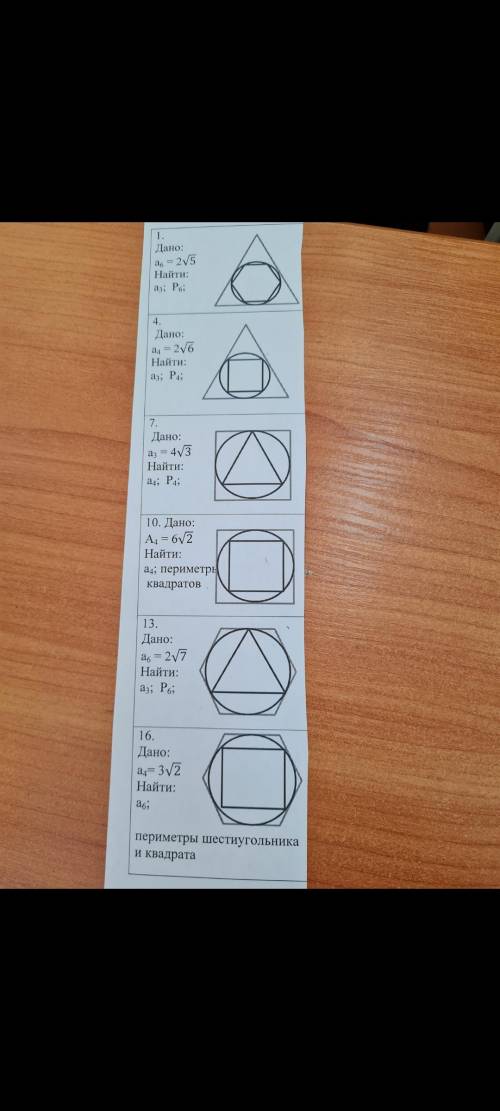
Другие вопросы по теме Геометрия
Популярные вопросы
- А)|x-1|=3 : )подробно..а то не как не могу решить(( б)(17x-68)*(3,7y-0,74)=0...
3 - Растают лелеем ударите услышим веет разрушите засеет реет .как будит в времени?...
2 - Почему семена называются зачаточными растениями?...
1 - Найди натуральное решение неравенства 9c 252...
1 - Как найти производную функции y=-3xtgx...
2 - Для устранения жесткости воды иногда применяют ортофосфат натрия.на чем основано...
3 - Гоголь. мертвые души. о чем рассуждает автор в 7 !...
1 - Сколько граммов муравьиной кислоты нужно для полной нейтрализации 20 г раствора...
3 - Реши пример.одинаковые буквы обозначают одинаковые цыфры. бра+бар=раб ток-кот=кто...
2 - 1.2*x+3*x+40 = 90 2. (х+40)-30=50 3. 70+(60-у)=130 4. 420-6х=240 5.-60: х=0,3...
1
Плохо відно
Объяснение:
На данной схеме видно, что вписанный четырехугольник (ABCD) и описанный вокруг него восьмигранник (A1B1C1D1E1F1G1H1). Задача состоит в том, чтобы определить, чему равны углы восьмиугольника A1B1C1D1E1F1G1H1.
Давайте решим эту задачу шаг за шагом:
Шаг 1: Воспользуемся свойством вписанного четырехугольника, согласно которому сумма противоположных углов равна 180 градусам. Поэтому угол A1C1B1 равен углу D1B1C1, а угол C1A1D1 равен углу B1D1A1.
Шаг 2: Посмотрим на триугольник A1B1D1. В нем сумма углов должна равняться 180 градусам. Поэтому угол A1B1D1 равен 180 - (угол A1C1B1 + угол C1A1D1).
Шаг 3: Так как сумма углов в треугольнике также равна 180 градусам, мы можем выразить угол B1 в треугольнике A1B1C1 через углы A1C1B1 и C1A1B1. Формула для этого будет следующей: угол B1 = 180 - (угол A1C1B1 + угол C1A1B1).
Шаг 4: Теперь мы знаем все углы A1B1D1 (полученный на шаге 2) и B1 (полученный на шаге 3). Чтобы найти уголы восьмиугольника, нужно вычислить оставшиеся углы в треугольнике B1C1D1 и домножить их на 2, так как восьмиугольник состоит из 8 равных треугольников.
Шаг 5: Поскольку триугольник B1C1D1 является равнобедренным (B1C1 = B1D1), мы можем вычислить угол C1B1D1 по формуле: угол C1B1D1 = (180 - угол B1D1) / 2.
Шаг 6: Теперь у нас есть все необходимые данные для вычисления углов восьмиугольника. Остается только подставить значения в формулу и выполнить все вычисления.
На этом завершилось решение задачи. Если у тебя есть еще вопросы по этой задаче или другим математическим вопросам, буду рад помочь!