8класс; доказать, что Абсд-параллелограмм. Решить задачи 9 и 12 с подробным решением или хотябы с объяснением. Заранее

Объяснение:

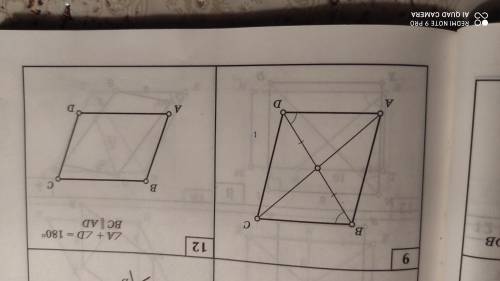
Задача 9

Обозначим точку пересечения диагоналей за О.(по дефолту)

Тогда треугольники ВОС и АОD равны(вертикальные углы, равные отмеченные углы и равные отрезки) по 2ому признаку. Отсюда АО = OD.

Таким образом диагонали в четырехугольнике делятся пополам => это параллелограмм.

Задача 12

Ну тут и так все написано, из первого условия => AB||CD (сумма односторонних углов 180). Также в условии дана параллельность двух других сторон. По определению этот четырехугольник параллелограмм.

В точке пересечения диагоналей, пусть это будет точка О,  образуются равные вертикальные углы, нас интересуют те, которые принадлежат треугольникам ВОС и АОD, и в этих же треугольниках углы СВО и ОDА равны. а так как они внутренние накрест лежащие, то прямые ВС и АD параллельны. треугольники равны по 2 признаку равенства. значит, ВС=АD и параллельны по признаку параллелограмма, т.к. пара сторон равна и параллельна, требуемое доказано.

12. ∠А+∠D=180°, а это сумма внутренних односторонних, значит, прямые АВ и СD, т.е. они параллельны, и по условию  ВС║АD то по определению АВСD- параллелограмм. ДОказано.