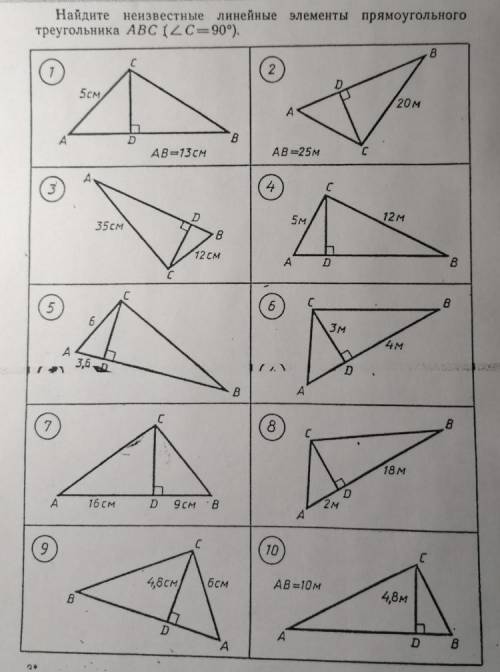
8кл найдите неизвестные линейные элементы прямоугольного треугольника abc [c= 90°).
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Пользователь вводит с клавиатуры два числа. Вывести в консоль отношение наибольшего...
3 - Составь уравнение прямой, проходящей через точку пересечения графиков линейных...
1 - Система средств, при которой строится связная звучная речь - это..?...
1 - сама не могу решить, буду благодарна ...
1 - Решите уравнение! а) log2^2х - 2log2x - 3 = 0 б) 2log6x + log6 49 = 2...
2 - Сколько это 10 %от 9 тысяч рублей. 10% то сколько денег...
3 - сделать задания. Упражнение 1. Подберите вопросительное слово. How How often (2)...
2 - 298°. Дано куб ABCDA, B,C,D, На- звіть:а) дві прямі, перпендикулярні до пло-щини...
3 - помагите Вопрос 1Пока нет ответа : 1Отметить вопросТекст вопросаАллотропной модификацией...
3 - Where was Usain Bolt competing (Usain Bolt/ compete) when he won (he/win) his firstOlympic...
1
Дано:
Угол C равен 90°.
Задача:
Найти неизвестные линейные элементы треугольника ABC.
Решение:
1. Известно, что в прямоугольных треугольниках гипотенуза является самой длинной стороной, и она соединяет две катеты.
2. Назовем стороны треугольника ABC следующим образом:
- гипотенуза (г) - сторона AC;
- катет (a) - сторона AB;
- катет (b) - сторона BC.
3. По теореме Пифагора, в прямоугольных треугольниках сумма квадратов катетов равна квадрату гипотенузы, то есть a^2 + b^2 = c^2.
4. Заменим известные значения в формулу Пифагора:
a^2 + b^2 = c^2
AB^2 + BC^2 = AC^2
5. Подставим известные значения в уравнение:
AB^2 + 9^2 = 15^2
AB^2 + 81 = 225
6. Перенесем 81 на другую сторону:
AB^2 = 225 - 81
AB^2 = 144
7. Извлекаем квадратный корень из обеих сторон уравнения:
AB = √144
AB = 12
8. Таким образом, сторона AB равна 12.
9. Для нахождения стороны BC, мы можем использовать теорему Пифагора снова:
AB^2 + BC^2 = AC^2
12^2 + BC^2 = 15^2
144 + BC^2 = 225
10. Переносим 144 на другую сторону:
BC^2 = 225 - 144
BC^2 = 81
11. Извлекаем квадратный корень из обеих сторон уравнения:
BC = √81
BC = 9
12. Таким образом, сторона BC равна 9.
13. Чтобы найти гипотенузу AC, мы можем использовать любую известную сторону и теорему Пифагора:
AC^2 = AB^2 + BC^2
AC^2 = 12^2 + 9^2
AC^2 = 144 + 81
AC^2 = 225
14. Извлекаем квадратный корень из обеих сторон уравнения:
AC = √225
AC = 15
15. Таким образом, гипотенуза AC равна 15.
Ответ:
Сторона AB равна 12, сторона BC равна 9, гипотенуза AC равна 15.