7 класс
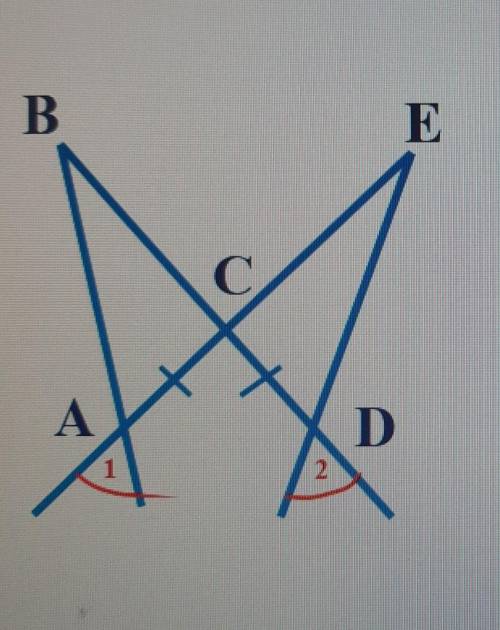
Дано: AC=CD , <1=<2
Довести: треугольник ABC= треугольнику DEC​

Для доказательства равенства треугольников ABC и DEC нам понадобится использовать свойства треугольников и равенство сторон и углов.

1. В данной задаче нам дано, что AC = CD, что означает, что отрезки AC и CD равны друг другу.

2. Также нам дано, что угол 1 равен углу 2 (углы 1 и 2 обозначены соответственно в треугольнике ABC и треугольнике DEC).

Исходя из этого, мы можем провести следующие шаги:

Шаг 1: Заметим, что AC = CD. Мы можем использовать это равенство для построения двух равных отрезков AC и CD в треугольнике DEC.

Шаг 2: Проведем отрезок AE, соединяющий вершины A и E. Теперь мы имеем два равенства: AC = CD и AC = CE, так как это один и тот же отрезок.

Шаг 3: Сравним две полученные треугольники: треугольник ABC и треугольник AEC. У них одинаковые стороны AC=AC и CE=CD (так как AC=CD).

Шаг 4: Посмотрим на углы этих треугольников. У нас есть два равных угла (углы 1 и 2), и мы также можем заметить, что угол BAC равен углу EAC. Поскольку мы имеем два равных угла и две равных стороны (по соответственности), мы можем сделать вывод, что треугольники ABC и AEC равны друг другу по критерию SSA (сторона-сторона-угол).

Шаг 5: Теперь, обратимся к треугольникам ABC и DEC. Мы уже доказали, что треугольники ABC и AEC равны друг другу. Из равенства треугольников ABC и AEC и равенства треугольников AC=CD и AC=CE, мы можем заключить, что треугольники ABC и DEC также равны друг другу по критерию SSS (сторона-сторона-сторона).

Таким образом, мы доказали, что треугольник ABC равен треугольнику DEC по критерию SSS, используя равенство сторон AC=CD и углов <1 = <2.