1. Геометрия
  2. 7. Катеты прямоугольного

7. Катеты прямоугольного равнобедренного треугольника ABC равны 10 дм. Из вершины прямого угла спроведён отрезок CD, перпендикулярный
плоскости этого треугольника. Найдите расстояние от точки D до гипотенузы
AB, если отрезок CD равен 12 см.​

whitesnaff whitesnaff    2   16.06.2021 07:46    0

Ответы
leha262006 leha262006  16.07.2021 08:47

переведём все размеры в единые единицы 10 дм = 100 см

по теореме Пифагора находим

AB=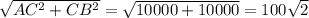\sqrt{AC^2 + CB^2} =\sqrt{10000+10000} = 100\sqrt{2}

Т.к. ABC равнобедренный AK=KB = 50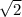\sqrt{2}

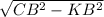
CK=\sqrt{CB^2 - KB^2}

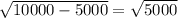
CK=\sqrt{10000-5000} = \sqrt{5000}

KD=\sqrt{CD^2+CK^2} = \sqrt{144+5000} =\sqrt{5144}=2\sqrt{1286}

 


7. Катеты прямоугольного равнобедренного треугольника ABC равны 10 дм. Из вершины прямого угла спров
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
dilyaramazhitova dilyaramazhitova  26.05.2019 11:30
Только развернутый ответ на бумажечке радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30 градусов. найдите а) площадь сечения коонуса...
ВладиславПрокофьев ВладиславПрокофьев  26.05.2019 11:30
Стороны ав и вс прямоугольника abcd равны 6см и 8 см. прямая, проходящая через вершину с и перпендикулярная к прямой bd, пересекает сторону ad в точке м, а диагональ вd в...
глупыйлолик34 глупыйлолик34  26.05.2019 11:30
Визначте кількість сторін правильного многокутника в якому: 1. центральний кут дорівнює 30 градусів? 2. сума кутів дорівнює 1800 градусів?...
nexsting1 nexsting1  26.05.2019 11:30
Abo-треугольник ав=14 см,во=21см,оо1=18см,найти высоту ао2 ао2 высота к основанию во,оо1 высота к основанию ав...
osadchevasasha osadchevasasha  26.05.2019 11:30
Втреугольника авс угол с = 90 градусов, tg a = √15. найдите cos a...
FarLime FarLime  26.05.2019 11:30
Вкубе abcda1b1c1d1 точка e - середина a1b1. найти cos между прямыми ae и bd1...
AmiKot1105 AmiKot1105  26.05.2019 11:20
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. найдите радиус описанной окружности этого треугольника....
25182830 25182830  26.05.2019 11:20
Найдите углы параллелограмма если известно, что один из них а) равен 10 градусов б) в пять раз больше другого...
oligayaraya oligayaraya  26.05.2019 11:20
Отрезки ac и bd пересекаются в середине o отрезка ac углы bco=dao. докажите что треугольники bao=doc....
Vitalikprofi Vitalikprofi  26.05.2019 11:20
Начертить окружность заданную уравнением: 1. x2+у2=4 2. (х+4)2+(у+3)2=9 3. (х-1)2+(у+2)2=25 4. (х-5)2+(у-2)2=16 5. (х+3)2+(у-4)2=4 6. х2+(у-3)2=16 7. (х+5)2+у2=25 8. х2+у2=5...

Популярные вопросы