1. Геометрия
  2. 60 вершины треугольника

60 вершины треугольника abc имеют координаты a(-2,0,1), b(-1,2,3) c( 8,-4,9). найти периметр и площадь треугольника

Dragon4ik341234 Dragon4ik341234    1   27.05.2019 22:22    1

Ответы
rassvetmoydrug rassvetmoydrug  25.06.2020 08:44

Определим координаты сторон треугольника (от координат конца вычитаем координаты начала):

AB(1; 2; 2); \ BC (9; -6; 6); \ AC (10; -4; 8)

Найдём длину стороны:

AB = \sqrt{1^{2} + 2^{2} + 2^{2}} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3

BC = \sqrt{9^{2} + (-6)^{2} + 6^{2}} = \sqrt{81 + 36 + 36} = \sqrt{153} = 3\sqrt{17}

AC = \sqrt{10^{2} + (-4)^{2} + 8^{2}} = \sqrt{100 + 16 + 64} = \sqrt{180} = 6\sqrt{5}

Отсюда периметр равен:

P = AB + BC + AC = 3 + 3\sqrt{17} + 6\sqrt{5}

Определим площадь треугольника по формуле Герона:

p = \dfrac{P}{2} = \dfrac{3 + 3\sqrt{17} + 6\sqrt{5}}{2}

S = \sqrt{p(p - AB)(p-BC)(p-AC)} =\\\\= \sqrt{\dfrac{3 + 3\sqrt{17} + 6\sqrt{5}}{2} \bigg(\dfrac{3 + 3\sqrt{17} + 6\sqrt{5}}{2} - 3 \bigg)\bigg(\dfrac{3 + 3\sqrt{17} + 6\sqrt{5}}{2} - 3\sqrt{17}\bigg)\bigg(3 + 3\sqrt{17} + 6\sqrt{5}}{2} - 6\sqrt{5} \bigg)} = 18

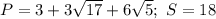
ответ: P = 3 + 3\sqrt{17} + 6\sqrt{5}; \ S = 18

Замечание. Вычисление площади треугольника упущено, ответ точный.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Smazi Smazi  13.07.2019 04:30
Площадь трапеции с основаниями 16 и 14 см равна 240 см^2. чему равна высота трапеции? а) 8 см б) 32 см в) 40 см г) 16 см...
dinadaybert dinadaybert  13.07.2019 04:30
Боковая сторона равнобедренного треугольника равна 17 см, а основание-16 см.найдите высоту, проведенную к основанию....
ksdaga ksdaga  13.07.2019 04:20
Найдите высоту равнобокой трапеции с основаниями 6см и 14см, если боковая сторона равна 5см...
Raphael1111 Raphael1111  13.07.2019 04:20
Бисектриса проведенная из вершины равнобедренного треугольника равна 5 см. периметр одног из образованных треугольников равен 30 см. найдите периметр данного равнобедренного...
ELB2 ELB2  13.07.2019 04:20
Основание твапеции равны 3и 15,боковая сторона равна 2,образует с одним из оснований трапеции угол 150°.найдите площядь трапеции...
natakhafedotovp06k9x natakhafedotovp06k9x  13.07.2019 04:20
Запишите уравнение окружности с центром в точке с(-3,-5) , r=1...
kulagindemid20 kulagindemid20  13.07.2019 04:20
За ответ 20 как научится решать быстро по...
Kpoper772 Kpoper772  13.07.2019 04:20
Периметр параллелограмма равен 80 см, одна из его сторон в 4 раза больше другой. найдите меньшую сторону параллелограмма....
Pomogiteπ Pomogiteπ  13.07.2019 04:20
Дано: abcd равнобедренная трапеция ab=cd=10 см bc=8см ad=20 см найти площадь...
DarvinaDark DarvinaDark  13.07.2019 04:20
Втреугольниках авс и а1в1с1 проведены биссектрисы ад и а1д1.докажите,что треугольник авс= треугольнику а1в1с1 если д1с1 ,угол с = углу с 1,угол адс= углу а1д1с1...

Популярные вопросы