6. Определите центр и радиус окружности, заданной уравнение 1) (x - 2)^2 +(у - 5)^2=7^2; 2) (x+1) ^2 + (у - 5)^2=4,
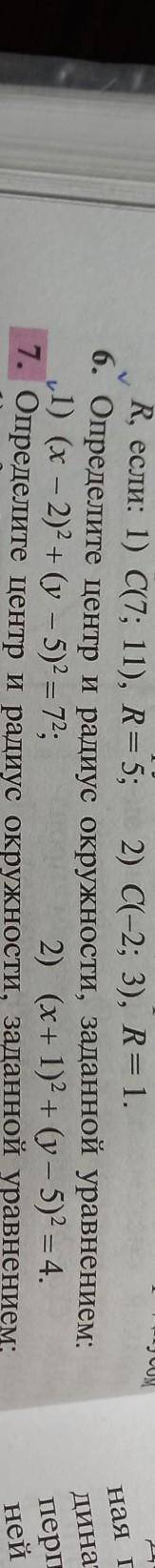
Другие вопросы по теме Геометрия
Популярные вопросы
- Хозяин ресторана планирует приобрести картофель на рынке или в овощном магазине....
3 - Определите горные породы по их свойствам пёстрые тяжёлые породы,состоящие из...
3 - Подберите синонимы с не к данным словам. сомнение, болезнь, ложь, беда, противник,...
1 - Сочинение по картине ивана ивановича фирсова...
1 - Иррациональное уравнение: (х²-144)*√(22х+13)=0...
2 - Сколько сантиметров в сотой части километра?...
2 - Какие части речи: если, хочешь, победить, весь, мир, победи, себя .какие части...
2 - Какой падеж у слов немцы,в сумке,на фронте....
3 - Написать приглашение на праздник, на языке. вопрос на стр. 20 в рабочей тетради...
3 - Никита копил деньги на новый телефон.в апреле цена телефона сначала снизилась...
2
1) Уравнение окружности (x - 2)^2 + (у - 5)^2 = 7^2 описывает окружность с центром в точке (2, 5) и радиусом 7.
Для определения центра и радиуса окружности из уравнения, мы должны привести его к стандартному уравнению окружности:
(x - a)^2 + (у - b)^2 = r^2, где (a, b) - координаты центра окружности, r - радиус окружности.
2) Уравнение окружности (x+1)^2 + (у - 5)^2 = 4 описывает окружность с центром в точке (-1, 5) и радиусом 2.
Теперь разберемся, как мы получаем эти результаты. Для этого перепишем исходные уравнения в стандартной форме:
1) (x - 2)^2 + (у - 5)^2 = 7^2
Раскроем скобки:
x^2 - 4x + 4 + у^2 - 10у + 25 = 49
Приведем подобные члены:
x^2 + у^2 - 4x - 10у + 29 = 49
Перенесем 29 на другую сторону:
x^2 + у^2 - 4x - 10у = 49 - 29
x^2 + у^2 - 4x - 10у = 20
Теперь сгруппируем по переменным:
(x^2 - 4x) + (у^2 - 10у) = 20
Выделим полные квадраты в скобках, добавив и вычтя соответствующие константы:
(x^2 - 4x + 4) + (у^2 - 10у + 25) = 20 + 4 + 25
(x - 2)^2 + (у - 5)^2 = 49
Таким образом, мы получаем уравнение окружности в стандартной форме. Мы видим, что координаты центра равны (2, 5), а радиус равен 7.
2) (x+1)^2 + (у - 5)^2 = 4
Раскроем скобки:
x^2 + 2x + 1 + у^2 - 10у + 25 = 4
Приведем подобные члены:
x^2 + у^2 + 2x - 10у + 26 = 4
Перенесем 26 на другую сторону:
x^2 + у^2 + 2x - 10у = 4 - 26
x^2 + у^2 + 2x - 10у = -22
Сгруппируем по переменным:
(x^2 + 2x) + (у^2 - 10у) = -22
Выделим полные квадраты в скобках, добавив и вычтя соответствующие константы:
(x^2 + 2x + 1) + (у^2 - 10у + 25) = -22 + 1 + 25
(x + 1)^2 + (у - 5)^2 = 4
Таким образом, мы получаем уравнение окружности в стандартной форме. Мы видим, что координаты центра равны (-1, 5), а радиус равен 2.
Надеюсь, это помогло вам понять, как определить центр и радиус окружности по заданному уравнению. Если у вас есть еще вопросы, не стесняйтесь задавать!