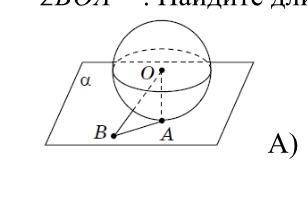
5. Шар с центром в точке О касается плоскости альфа в точке А (рисунок). Точка В лежит в плоскости альфа, причем AB = d, ∠BOA = бэта. Найдите длину отрезка ВO
А) d tg​Б) d sin​​В) d cos​ Г) ​d ctg

Для решения данной задачи, нужно использовать свойства окружностей и треугольников, а также знания о тригонометрии.

Из условия задачи видно, что шар с центром в точке О касается плоскости альфа в точке А. Также дано, что точка В лежит в плоскости альфа, причем AB = d и ∠BOA = бэта.

1. Обратимся к правилу касательной, которое гласит, что касательная, проведенная к окружности в точке касания, является перпендикуляром к радиусу, проведенному в точку касания. Таким образом, отрезок АО является перпендикуляром к плоскости альфа.

2. Рассмотрим треугольник АВО. Так как отрезок АО является перпендикуляром к плоскости альфа, то он будет перпендикулярен отрезку AB.

3. Теперь рассмотрим прямоугольный треугольник АВО. Мы знаем, что ∠BOA = бэта, поэтому отрезок АВ будет гипотенузой данного треугольника, отрезок АО - противоположным катетом, искомый отрезок BO - смежным катетом.

4. Косинус угла в прямоугольном треугольнике определяется соотношением cos = прилежащий катет / гипотенуза. В нашем случае cos бэта = BO / AB.

5. Для решения задачи, необходимо выразить BO через AB. Так как AB = d, то мы можем переписать наше уравнение как cos бэта = BO / d.

6. Разрешим полученное уравнение относительно BO: BO = d * cos бэта.

Таким образом, длина отрезка ВО равна d * cos бэта.

Ответ: В) d cos бэта.