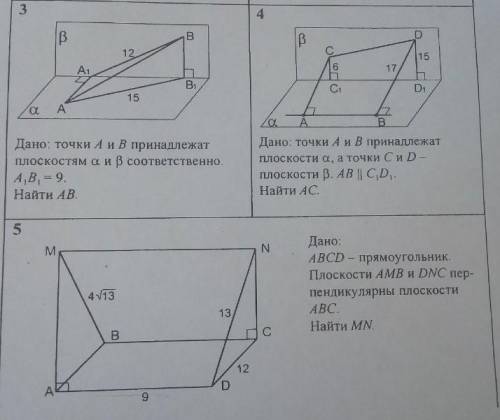
4 задача: Дано: точки A и B принадлежат плоскости альфа, а точки C и D -плоскости бетта. AB параллельно C1D1 Найти: AC . 5 задача: abcd прямоугольник плоскости amb и dnc перпендикулярны плоскости abc найти mn
Другие вопросы по теме Геометрия
Популярные вопросы
- Человек в течении суток теряет много литров воды Сколько литров воды нужно...
3 - РЕШИТЬ. Пытался сам не получается,буду очень благодарен...
2 - с английским задние на фото 40б...
1 - 18 x 1 2/3 х 0,4 + 6 х 1 2/3 - 24 х 0,4 - 8...
1 - Как подключить блютуз наушники к ноутбуку...
2 - увеличение площади поверхности листа растений приводит к : а)нарушению...
3 - 7. Задача. У понеділок у шкільній ідальні використали 4,2 кг борошна, що...
2 - В пищеварительном системе речного рака пища измельчается ПРАВИЛЬНЫЙ ОТВЕТ...
1 - решить задание по английскому языку...
1 - Посмотрите дайте ответ правильный это контрольная работа ...
1
4 задача:
У нас есть точки A и B, которые принадлежат плоскости альфа, и точки C и D, которые принадлежат плоскости бетта. Мы знаем, что AB параллельно C1D1. Нам нужно найти длину отрезка AC.
Чтобы решить эту задачу, нам понадобится использовать свойство параллельных прямых. Если две прямые параллельны, то у них все углы равны. В нашем случае, мы видим, что AB параллельно C1D1.
Таким образом, у нас есть два параллельных отрезка: AB и C1D1. Значит, у этих отрезков все углы будут равны.
Теперь мы можем использовать свойство треугольника, которое говорит, что сумма углов треугольника равна 180 градусам. Так как ACB и C1D1B - параллельные треугольники, то их сумма углов будет равна 180 градусам.
Давайте обозначим угол CAB = α и угол C1DB = β. Таким образом, у нас есть два уравнения:
α + β = 180 градусов (уравнение 1)
∠ACB = α (уравнение 2)
Теперь мы можем решить уравнение 1 относительно β и подставить его в уравнение 2:
β = 180 - α
∠ACB = α
Теперь давайте рассмотрим треугольник ABC. Мы знаем, что сумма углов треугольника равна 180 градусам. Так как у нас есть угол α и угол ∠ACB (который равен α), то мы можем найти третий угол треугольника.
Угол BAC + α + α = 180 градусов
2α + β = 180 градусов
2α + (180 - α) = 180 градусов
2α + 180 - α = 180 градусов
α + 180 = 180 градусов
α = 0 градусов
Таким образом, мы получили, что α = 0 градусов. Это значит, что угол CAB несуществующий, что невозможно. Мы сделали ошибку в решении этой задачи. Вероятно, была допущена ошибка в условии или в построении в задаче.
5 задача:
У нас есть прямоугольник ABCD, который лежит в плоскости amb. Мы также знаем, что прямые amb и dnc перпендикулярны прямой abc. Нам нужно найти длину отрезка mn.
Чтобы решить эту задачу, нам понадобится использовать свойство перпендикулярных прямых. Если две прямые перпендикулярны, то их углы будут равны 90 градусов. В нашем случае, мы видим, что прямая amb перпендикулярна прямой dnc.
Таким образом, у нас есть три перпендикулярных отрезка: amb, dnc и abc. Значит, у этих отрезков все углы будут равны 90 градусов.
Теперь давайте обозначим угол MAB = α и угол MDC = β. Таким образом, у нас есть два уравнения:
∠MAB = α (уравнение 1)
∠MDC = β (уравнение 2)
Теперь мы можем использовать свойство треугольника, которое говорит, что сумма углов треугольника равна 180 градусам. Так как MA и MD - прямые линии, то сумма их углов равна 180 градусам.
Теперь давайте рассмотрим треугольник AMD. Мы знаем, что сумма углов треугольника равна 180 градусам. Так как у нас есть угол α и угол β, то мы можем найти третий угол треугольника.
Угол AMD + α + β = 180 градусов
90 градусов + α + β = 180 градусов
α + β = 90 градусов
Таким образом, мы получили, что α + β = 90 градусов. Нам нужно найти длину отрезка mn. Однако, нам не даны дополнительные данные о прямоугольнике ABCD для нахождения этой длины. Поэтому ответ на эту задачу нельзя найти без дополнительных данных.
Итак, в обоих задачах у нас возникли проблемы с условием или построением, и нам не удалось найти итоговый ответ. Если вам нужно, я могу объяснить множество других математических концепций или помочь с другими задачами.