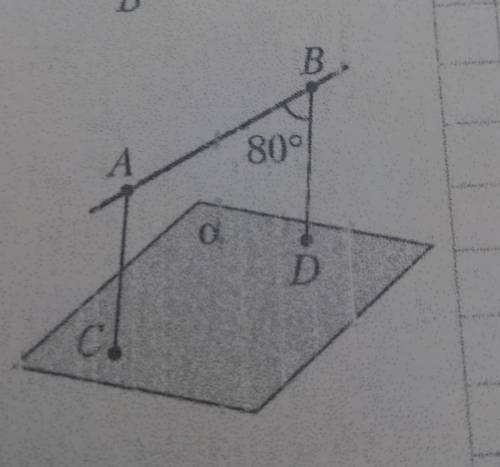
4. Точки Си D принадлежат плоскости a, AB | C, AВ || а, угол ABD = 80°. Найдите величину угла ACD.
Другие вопросы по теме Геометрия
Популярные вопросы
- Синтаксический разбор предложения он вышел на улицу и наткнулся...
3 - Установить связь: калий-хлортд калия-гидроксид калия--сульфат бария...
2 - Неравенства с 1 переменной 3x - 4≥5 , 2x+3≤4x-3 , 2( x-3) 3 ( x...
1 - Навеснi прокдаеться природа вiд зимового сну. вiтер шелестить у...
2 - Найди словосочетание, в котором имя прилагательное употреблено...
2 - Выберите меры компьютерных преступлений 1)использование свободного...
3 - Наименьшоее натуральное число которое делится на 4 и на 6...
2 - Сколько лет живьот черипаха сколько лет ето пройдьот для человека...
2 - Скакой целью в атлас включены карты...
2 - Решить . два самолета летели с одинаковой скоростью . первый самолет...
3
В данной задаче, мы имеем следующие условия:
1. AB | C - прямая AB параллельна прямой C.
2. AB || а - прямая AB параллельна плоскости а.
3. угол ABD = 80°.
Теперь рассмотрим треугольник ACD. У нас есть две параллельные прямые AD и AB, а также сторона AC. Следовательно, это треугольник, возможно, прямоугольный или подобный.
Но перед тем, как мы найдем угол ACD, нам понадобится еще одна информация о треугольнике ABD.
Из условия задачи, у нас имеется угол ABD = 80°. Это полезно для нахождения других углов треугольника ABD.
Известный нам угол ABD = 80°.
Теперь решим задачу:
1. Угол ABC = угол ABD (по определению параллельности прямых) = 80°.
2. Угол BAC = 180° - угол ABC - угол ACB (сумма углов треугольника) = 180° - 80° - 180° = 100°.
3. Треугольник ABC - неравнобедренный треугольник, поэтому угол BCA (угол между C и AB) = угол BAC = 100°.
4. Треугольник ACD подобен треугольнику ABC по признаку общего соотношения углов треугольников.
5. Угол ACD = угол ACB (по свойству подобных треугольников) = 100°.
Итак, величина угла ACD равна 100°.