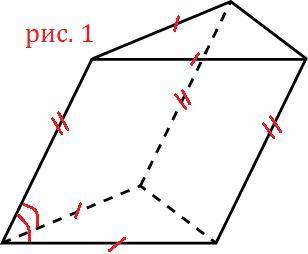
№4.1. Дана треугольная призма у которой две боковые грани являются равными параллелограммами (см. рис. 1). Докажите, что третья боковая грань это прямоугольник.
Другие вопросы по теме Геометрия
Популярные вопросы
- Закончи фразу. длина диаметра окружности с центром в точке р равна...
3 - №20.в первую строчку впиши первое словарное слово,поставив его в форму ед.ч.п.п.с...
3 - Найдите значение выражение 5х - 9 при х равно 2 целых 1/2 дробью...
1 - Какие возможны коррозионные процессы,если на поверхности детали из углеродистой...
2 - Найдите первый член и разность арифметической прогрессии (an), если а7+а3=-8,...
2 - Решите : из двух городов одновременно навстречу друг-другу вышли два поезда и...
1 - Дана правильная четырехугольная пирамида высота которой равна 12 см а апофема...
2 - Очем рассказывает в мифе об осирисе и исиде ? ? 5 класс тетрадь для проектов и...
2 - Решите в развенутом виде - всмысле ну не просто написать ответы нужно ,а еще как...
3 - Сколько составляет подоходный налог от зарплаты 9190...
3
Что и требовалось доказать.
Объяснение:Обозначим данную треугольную призму буквами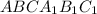 .
.
По чертежу определяем, что :
Проведём высоту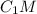 к стороне
к стороне  в
в 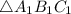 .
.
Также проведём высоту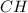 данной треугольной призмы.
данной треугольной призмы.
Так как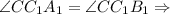 основание высоты
основание высоты 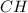 данной призмы лежит на высоте
данной призмы лежит на высоте 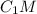 .
.
Это значит, что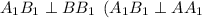 соответственно
соответственно .
.