35 . мотоциклист проехал по замкнотому пути abca такому что abc- прямоугольный треугольник с катетами ab и bc причем ab+1=bc. по участкам ab и bc мотоциклист ехал со скоростью 41 км в час а на промежутке ca пошёл дождь и скорость была снижена до 29 км в час . в результате на путь abc вдоль катетов треугольников он затратил столько же времени сколько на гипотенузу ca. определить длину abca пройденного мотоциклистом

Длина АВСА равна 70 км

Объяснение:

Пусть АВ = х, тогда

ВС = х + 1

По теореме Пифагора АС² = АВ² + ВС² = 2х² + 2х + 1

- время прохождения АВ

- время прохождения ВС

-время прохождения АС

По условию

Решаем уравнение

29² · (2x + 1)² = 41² · (2x² + 2x + 1)

841 · (4x² + 4x + 1) = 1681 · (2x² + 2x + 1)

3364x² + 3364x + 841 = 3362x² + 3362x + 1681

2x² + 2x - 840 = 0

x² + x - 420 = 0

D = 1 + 1680 = 1681

√D = 41

x₁ = 0.5 · (-1 - 41) = -21  - не подходит по физическому смыслу расстояния

х₂ = 0,5 · (-1 + 41) = 20

Итак, АВ = х = 20 (км)  

ВС = х + 1 = 21 (км)

АС =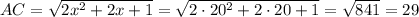 (км)

Весь путь АВСА  S = АВ + ВС + АС = 20 + 21 + 29 = 70 (км)