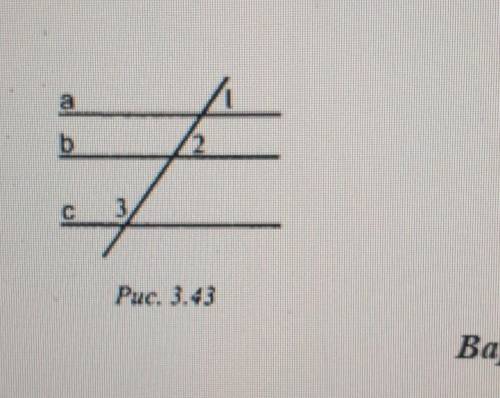
3. Рис. 3.43.
Дано: угол 1 = угол2; угол2+ угол3 = 180°.
Доказать: a | с.​

ответ: Я не знаю

Объяснение: Простите

Для доказательства того, что прямые a и c являются параллельными, мы можем использовать свойство параллельных линий, которое гласит: "Если две прямые пересекают третью прямую так, что сумма внутренних углов на одной стороне равна 180 градусам, то эти две прямые параллельны". Другими словами, если углы 2 и 3 находятся по одну сторону от прямой a и их сумма равна 180 градусам, то прямая a параллельна прямой c.

Исходя из данной информации, у нас имеются следующие данные: угол 1 = угол 2 и угол 2 + угол 3 = 180 градусов. Чтобы доказать, что прямые a и c параллельны, мы должны использовать эти данные и логическую цепочку рассуждений.

1. По условию дано, что угол 1 равен углу 2, то есть угол 1 = угол 2.
2. Также дано, что сумма угла 2 и угла 3 равна 180 градусам, то есть угол 2 + угол 3 = 180°.
3. Подставляем значение угла 2 из первого шага в уравнение второго шага: угол 1 + угол 3 = 180 градусов.
4. Теперь мы можем видеть, что в уравнении есть угол 1, который равен углу 2, и угол 3. Мы знаем, что в сумме они равны 180 градусам.
5. Таким образом, мы можем заключить, что угол 1 + угол 3 составляют сумму внутренних углов на одной стороне от прямой a, которая равна 180 градусам.
6. Согласно свойству параллельных линий, если сумма внутренних углов на одной стороне от прямой равна 180 градусам, то эта прямая параллельна другой прямой, пересекающей третью прямую.
7. В нашем случае это означает, что прямые a и c являются параллельными.

Таким образом, мы доказали, что прямые a и c параллельны на основе данных об углах 1, 2 и 3, предоставленных на рисунке 3.43.